Prírodou inšpirované algoritmy

Diskrétny model

Pri diskrétnom riešení sústavy diferenciálnych rovníc, tvoriacich model Lotka-Volterra dochádza k ich diskretizácii. Tento proces je v istom zmysle bližšie k realite, nakoľko počty jedincov v populácii ako aj zrod a uhynutie jedinca majú diskrétny charakter. V (Peitegen & Richter, 1986) je navrhnutá zaujímavá kombinácia dvoch jednotkových numerických metód - Eulerovej a Heunovej. Ak v spojitom modeli Lotka-Volterra zavedieme označenie:

dK/dt = a * K - b * K * D = f(K,D)
dD/dt = c * K * D - d * D = g(K,D)

potom kombinované numerické riešenie má tvar:

Kn+1=Kn + h/2*[f(Kn, Dn) + f[Kn + p*f(Kn, Dn), Dn + p*g(Kn, Dn)]]
Dn+1=Dn + h/2*[g(Kn, Dn) + g[Kn + p*f(Kn, Dn), Dn + p*g(Kn, Dn)]]

V nasledujúcom obrázku prevzatom z (Peitegen & Richter, 1986) je rovina p=h rozdelená na 4 oblasti, charakterizované zásadne odlišnou dynamikou iteračného procesu:

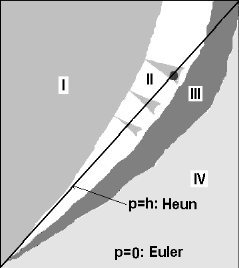
I. bod (1, 1) je atraktorom, ku ktoré­mu konvergujú všetky orbity,

II. atraktorom je uzavretá krivka - invariantný cyklus (príklad) - ku ktorému konvergujú orbity z vnútornej aj vonkajšej strany (body na tomto atraktore netvoria nejakú pravidelnú postupnosť - keby sme ich spojili lomenou čiarou, vytvorili by nepravidelnú hviezdicu, podobnú tejto),

III. podivný atraktor (obr. a obr.),

IV. neexistuje atraktor okrem nekonečna (iterácia diverguje).

Prechod z oblasti I. do II. možno interpretovať ako zmenu stabilného bodu na nekonečne malý invariantný cyklus, pričom konvergencia je v blízkosti tohoto prechodu veľmi pomalá. V oblasti II. existuje nekonečne veľa úzkych jazykov, vymedzujúcich podoblasť II*, pre ktorú okrem invariantného cyklu existuje aj ďalší atraktor, tvorený konečným počtom izolovaných bodov. Takýmto prípadom je p = h = ­0.73 (čierny bod na grafe). Na nasledujúcom obrázku vľavo (detail) je pre tento prípad orbita končiaca na invariantnom cykle, pričom počiatočná podmienka je blízka singulárnemu bodu (1,1). Na atraktore - invariantnom cykle - končia všetky orbity, začínajúce v bielej oblasti. Na druhom obrázku (detail) sú po sebe idúce body iterácií pospájané lomenou čiarou, teda je zrejmé, že body po atraktore nepravidelne "skáču". Na treťom obrázku (detail) je druhý atraktor, tvorený deviatimi bodmi. Na tomto atraktore končia všetky orbity, začínajúce v niektorej z deviatich červených plôšok, v ktorých ležia body atraktora.

Pri prechode z oblasti II. do III. je možné pozorovať „rozpad“ hraničného cyklu na konečný počet drobných plôšok, tvoriacich podivný atraktor – po doznení prechodových dejov sa body orbitu vyskytujú iba v týchto plôškach - štvrtý obrázok (detail). Pri ďalšom "posune" do oblasti III. sa tieto plôšky "roztiahnu" do čiar a podivný atraktor je tvorený ich čoraz zložitejšou spleťou - posledný obrázok (detail).

V ďalších podkapitolách sa podrobnejšie pojednáva o hraniciach oblastí a o jednotlivých oblastiach: I, II, III a IV

Pomocou appletu je možné si poexperimentovať s opísaným diskrétnym modelom. Rozsiahlejšie experimenty umožňuje samostatný program.