Prírodou inšpirované algoritmy

Oblasť I

Pre všetky body v oblasti I platí, že majú jediný atraktor (okrem nekonečna), do ktorého skonvergujú. Je ním bod (1, 1). Je to singulárny bod (asymptoticky nestabilný) pre diskretizované rovnice uvedené v kapitole Teória.
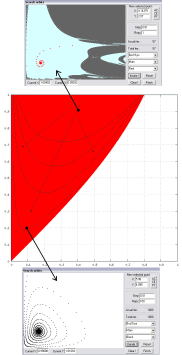
Ak odštartujeme iterácie pre akúkoľvek kombináciu parametrov (p, h) z danej oblasti, skončia všetky body v atraktore (1, 1). Jediný rozdiel medzi orbitami pre body z tejto oblasti bude v rýchlosti konvergencie k atraktoru. Rýchlosť konvergencie bodov v oblasti bude mať charakter vrstevníc ako na obrázku.

Krivky v strednej časti obrázka naznačujú vrstevnice rýchlosti konvergencie k atraktoru v smere šípok. V hornej časti (začiatok šípok) je konvergencia k atraktoru rýchlejšia ako na konci šípok, či v ľavom dolnom rohu roviny h-p. Horná a dolná časť obrázka (hore) názorne zobrazuje aká rýchla je konvergencia k atraktoru. Tieto obrázky sú vytvorené softvérom, ktorý bol na tento účel napísaný. Je na nich jasne vidieť rozdiel, ktorý popisujem vyššie. Konvergencia navrchu je pre parametre p = 0.9, h = 0.4 a spodný záber ukazuje rýchlosť konvergencie bodu roviny pre p = 0.2 a h = 0.1.