Prírodou inšpirované algoritmy

Oblasť IV

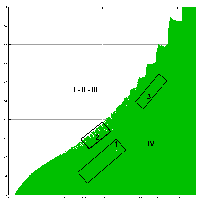
Všetky zdroje, ktoré sa venovali problematike diskretizovaného modelu Lotka-Volterra označili pre túto oblasť (obrázok dole) ako atraktor "nekonečno". Znamená to, že iterácie bodov divergujú do nekonečna. Rýchlosť divergencie je rôzna. Predpokladáme opäť vrstevnicovú formu rýchlosti divergencie ako v oblasti I. Podobné správanie možno pozorovať aj na Mandelbrotovej množine.

Oblasť nekonečna už ale nie je tak "čistá" (jednoliata) ako oblasť I. Pri podrobnejšom skúmaní nájdeme v tejto oblasti body, pre ktoré iteračný proces nediverguje. Na hornom obrázku sú to všetky biele miesta (body) na zelenom pozadí.

V nasledujúcom texte priblížime oblasť vyznačenú ako 1. O zostávajúcich dvoch oblastiach sa dočítate v (Ondáš, 2004).

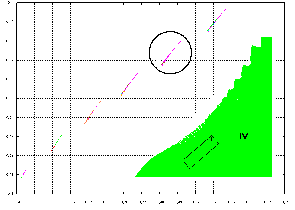
Oblasť 1 je veľmi zaujímavá. Vyzerá, ako časť nejakej tenkej čiary. V (Ondáš, 2004) autor študoval štruktúru bližšie a zistil, že to nie je čiara. Túto oblasť, ktorá je na obrázku dole, tvoria drobné čiarky, ktoré postupne smerom k (1, 1) v h-p sa stenšujú a pri použitom kroku 0.0001 zmeny parametrov p, h nakoniec zaniknú.

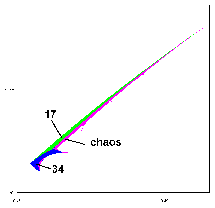
Výrez zakrúžkovanej oblasti je zobrazený na nasledujúcom obrázku (dole). Aj táto veľmi malá časť má charakter roztiahnutého zuba z II. Obsahuje cykly s periódami 17, 34, a invariantný cyklus. Vo všetkých hraničných oblastiach sú malé červené body, v ktorých bod s takýmito súradnicami obsahuje atraktor oboch spomenutých periód (viď výrez). Tieto body sú však podľa mojich testov veľmi nestabilné a časom sa ustália na jednej z dvoch individuálnych periód (17 alebo 34). Druhou možnosťou je, že hranica medzi farebnými oblasťami (periódy a invariantný cyklus) je tak tenká tenká čiara, že pri použitom rozlíšení ju nie je možné zobraziť ako čiaru, ale iba zachytiť len niektoré jej body . Na obrázkoch s periódami 17 a 34 je vidieť, že rozdiel medzi cyklami je veľmi nepatrný a z toho vyplýva aj autorove tvrdenie o červených bodoch.