Prírodou inšpirované algoritmy

Oblasť II

Podkapitoly:

Prechod z II do III
Koexiistencia - detaily

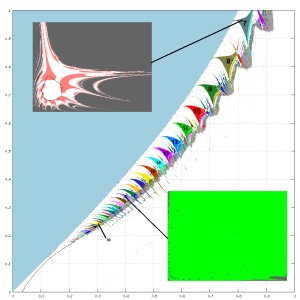
Najzaujímavejšou oblasťou pre štúdium je oblasť označená ako II. Už na prvý pohľad zaujme fraktálovou štruktúrou. Potvrdila sa prítomnosť zubov, ktoré načrtli už autori v (Peitegen & Richter, 1986). Bližšie štúdium podporilo aj tvrdenie, že počet počet zubov s periódami nie je konečný.

Podrobné štúdium oblasti potvrdilo všetky uverejnené výsledky na (Edwards,WWW). V nasledujúcom texte sú tieto fakty zhrnuté a neuvádza sa všade ich pôvod. Sú uvedené aj porovnania, spresnenia a nové poznatky.

Biela farba v oblasti II na výslednom obrázku roviny h-p predstavuje oblasť, pre ktorej body existuje jediný atraktor. Ním je invariantný cyklus. Body sa po takomto cykle pohybujú chaoticky. Na nasledujúcom obrázku vľavo je ukážka takéhoto cyklu aj s procesom ustálenia. Nápadne sa podobá Siegolovmu kotúču z Juliovej množiny (nasledujúci obrázok vpravo).

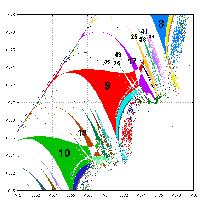
Veľkosti periód hlavných zubov (veľké) tvoria postupnosť smerom k (0, 0) v rovine h-p tak, ako je to vidno na ďalšom obrázku.

Smerom k (0, 0) veľkosť periódy atraktora narastá. Ako príklad sú uvedené dve periódy. 7 a 20. Na obrázku periódy 7 (p = 0.967, h = 0.822) sú body naviac pospájané čiarami. Iterácie štartovacieho bodu sa po čase ustália na siedmich hodnotách, ktoré sú stabilné - atraktor. Pre periódu 20 (p = 0.342, h = 0.4) platia rovnaké pravidlá. Zelená farba označuje oblasť, z ktorej ak z akéhokoľvek bodu odštartujem iteračný proces, po čase sa ustáli na cykle s periódou, ako to vidieť na obrázku. Na nasledujúcom obrázku sa nachádza atraktor s periódou 8 a 10. Pre periódu 8 (na obrázku vľavo) je nakreslený iba cyklus. Spolu s ním existuje aj invariantný cyklus (biela). Na obrázku vpravo je znázornený aj prechodový dej (malé žlté body). Po ustálení nebola kresliaca plocha nevymazaná, ale preponutím do režimu kreslenia čiar boli pre lepšiu názornosť spojené body atraktora do uzavretej krivky.

Pre ilustráciu poslúžia ďalšie dve periódy. 12 a 30.

Zub s periódou 7 nie je prvým v poradí. Je prvým iba v oblasti, ktorú ohraničuje zhora p = h = 1. Periódy s nižšími cyklami pokračujú do oblasti, ktorá nebola predmetom skúmania mojej diplomovej práce. Avšak autor na stránke (Edwards, WWW) skúmal aj oblasť mimo intervalu (0, 1) a potvrdil klesajúcu postupnosť periód tu.

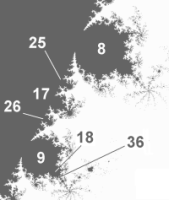
Nielen periódy hlavných zubov vykazujú postupnosť, ale aj menšie medzi nimi sa riadia presným pravidlom. Nemožno si nevšimnúť analógiu s Mandelbrotovou množinou. Pravidlo, ktoré platí medzi periódami hlavných zubov je jednoduché. "Perióda prostredného zuba je vždy súčtom jeho dvoch susedov".

Na obrázku vľavo sú schematicky naznačené tieto postupnosti medzi zubmi s periódou 8 a 9. Rovnaký charakter sa opakuje medzi všetkými zubmi. Pri zuboch s vyššou periódou ako 24 sa na obrázkoch už menšie zuby nevyskytujú, pretože boli testy periód obmedzené na 50.

Obrázok vpravo zobrazuje rovnakú vlastnosť na Mandelbrotovej množine.

Autor na (Edwards, WWW) upozorňuje ešte na jednu analógiu s Mandelbrotovou množinou. Rovina h-p má k príkladom v rovine x-y analogický vzťah ako má Madelbrotova množina k jednotlivým Juliovým množinám.

Práca (Ondáš, 2004) sa na hľadanie hranice medzi oblasťami II a III podľa pôvodného obrázka nesústredila, pretože túto hranicu je veľmi zložité stanoviť automaticky. Jej ohraničenie bolo urobené manuálne na základe experimentov. Na internetovej stránke (Edwards, WWW) autor zobrazuje oblasť III z obrázka autorov (Peitegen & Richter, 1986) ako čiernu oblasť (obr) a na tejto verzii ako oblasť označenú sivou farbou.

Nesporne veľmi zaujímavý je prechod z oblasti II do III, o ktorom viac v samostatnej podkapitole.

Výskum (Edwards, WWW) a táto analýza roviny h-p upozornila na koexistenciu viacerých atraktorov súčasne. Je možné nájsť kombináciu atraktora s presnou periódou spolu s invariantným cyklom. Výnimkou nie je ani kombinácia viacerých atraktorov s rôznou periódou v jednom obrázku bez prítomnosti invariantného cyklu. Na túto koexistenciu sa autor pozrel bližšie vo výreze zobrazenom v nasledujúcom obrázku.
Viac podrobností a ukážok v samostatnej podkapitole.

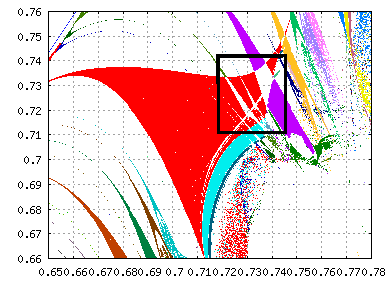
Za zmienku stoja aj zakončenia zubov a znásobovanie veľkosti periódy vo vnútri veľkého zuba, o ktorých je viac napísané v diplomovej práci.