Pri popisovaní obsahu obrazu je niekedy potrebné, závisí od
aplikácie, popísať tvary jednotlivých objektov spôsobom
invariantným voči natočeniu, zväčšeniu a pod., v iných
prípadoch takáto požiadavka nemusí existovať.
Je zrejmé, že pokiaľ reprezentácia vyhovuje tým prvým
prípadom, bude vyhovovať aj pre tie druhé. Práve z tohoto
dôvodu je efektívne sa zamerať na reprezentácie, ktoré sú
invariantné voči transformáciám.
Vo všeobecnosti, reprezentácie tvarov môžu byť rozdelené na
dve skupiny:
- boundary based - hľadanie hraníc medzi jednotlivými
homogénnymi oblasťami obrazu, postupným delením väčších
častí na menšie
- region based - hľadanie hraníc regiónov, pričom
postupujeme z vnútra regiónu smerom ku hraniciam regiónov
Podľa [64] by dobrá (t.j.. dobre použiteľná)
reprezentácia mala mať nasledujúce vlastnosti:
- Robustnosť voči transformáciám - reprezentácia by
mala byť invariantná voči posunutiu, rotácii a zmenám
mierky, podobne aj definícia štartovacieho bodu postupnosti
popisujúcej hranicu oblasti.
- Robustnosť voči šumu - reprezentácia musí byť odolná
voči priestorovej diskretizácii (spatial
discretization) šumu.
- Efektívna extrakcia vlastností - vektory príznakov by
mali byť vypočítané efektívne.
- Efektívne porovnanie príznakov - keďže porovnávanie
prebieha on-line, použitá metrika by mala vyžadovať
minimálne výpočtové náklady.
V ďalšom si popíšeme Fourierov deskriptor a modifikovaný
Fourierov deskriptor, ktoré spĺňajú vyššie spomenuté
podmienky a sú pomerne často používané v oblasti CBID.
Na začiatok je potrebné zadefinovať si v ďalšom používané
skratky a názvy:
- -
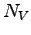 : počet vrcholov polygónu
: počet vrcholov polygónu
- -
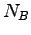 : počet hraničných bodov obrysu
: počet hraničných bodov obrysu
- -
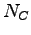 : počet FD koeficientov použitých
pri rekonštrukcii obrysu
: počet FD koeficientov použitých
pri rekonštrukcii obrysu
- -
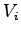 :
: 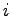 -tý vrchol polygónu
-tý vrchol polygónu
- -
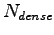 : počet ``dense'' vzoriek
použitých pri MFD
: počet ``dense'' vzoriek
použitých pri MFD
- -
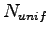 : počet uniformly spaced
vzoriek v MFD
: počet uniformly spaced
vzoriek v MFD
- -
-
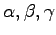 : planárne krivky
(tvary hraníc)
: planárne krivky
(tvary hraníc)
Subsections
Adrian Toth
2005-11-16