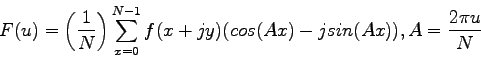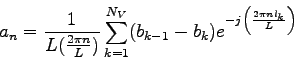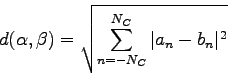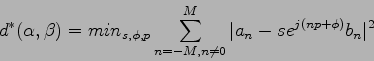Existujú dva všeobecne známe Fourierove deskriptory (FD),
popísané v [81] a
[57], budeme sa na nich odvolávať pod
skratkou ``FD1'' a ``FD2''.
Hodnoty Fourierových deskriptorov sú produkované Fourierovou
transformáciou časti obrazu obsahujúcej objekt vo
frekvenčnej oblasti. Deskriptory nižších frekvencií popisujú
hrubú informáciu o tvare, kým deskriptory vyšších
frekvencií popisujú detaily v obraze. Z toho vyplýva, že
komponenty nižších frekvencií definujú hrubý tvar pôvodného
objektu. Postup popisu tvaru je taký, že obraz, resp. jeho
časť sa premietne do roviny komplexných čísel. Tým pádom
súradnice každého bodu na hranici objektu môžu byť
vyjadrené ako komplexné číslo 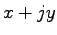 . Ak postupne prejdeme hranicou
pohybujúc sa proti smeru hodinových ručičiek konštantnou
rýchlosťou, dostaneme
postupnosť komplexných čísel, t.j. jednorozmernú funkciu
komplexnej premennej 3.6.
. Ak postupne prejdeme hranicou
pohybujúc sa proti smeru hodinových ručičiek konštantnou
rýchlosťou, dostaneme
postupnosť komplexných čísel, t.j. jednorozmernú funkciu
komplexnej premennej 3.6.
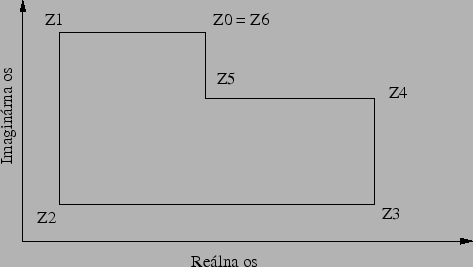
Obrázok:
Reprezentácia obrysu v komplexnej rovine
 |
Prechádzanie hranice viac ako raz nás vedie k periodickej
funkcii. Vychádzajúc zo vzťahu 3.10 a
3.8 a rozpísaním
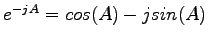 dostaneme
dostaneme
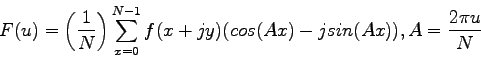 |
(3.41) |
Diskrétna Fourierova transformácia (DFT) postupnosti komplexných
čísel získaných prechodom cez hranicu určitého objektu nám
dáva hodnoty Fourierovho deskriptoru daného obrysu.
DFT je reverzibilná lineárna transformácia, takže zachovaná
pôvodnú informačnú hodnotu. Informácia získaná po
transformácii je v takom tvare, ktorá nám umožní izolovať
rôzne nežiaduce faktory, dokonca existuje možnosť úplného
odstránenia takýchto faktorov. V tomto zmysle, hodnoty
Fourierovho deskriptora môžu byť normalizované, tým dosiahneme
nezávislosť transformácie od posunu, zväčšenia a natočenia
pôvodného obrysu.
Posun obrysu o nejaké komplexné číslo, ktoré má zložky 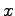 a
a
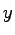 , zodpovedá matematickej operácii súčtu konštanty
, zodpovedá matematickej operácii súčtu konštanty 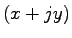 s každým prvkom obrysu. V prípade DFT má posun pomocou
takejto konštanty vplyv na koeficient
s každým prvkom obrysu. V prípade DFT má posun pomocou
takejto konštanty vplyv na koeficient 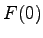 vo Fourierovom
rade. Preto normalizáciu pozície uskutočníme splnením
požiadavky
vo Fourierovom
rade. Preto normalizáciu pozície uskutočníme splnením
požiadavky 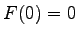 .
.
Úpravu mierky dosiahneme vynásobením všetkých prvkov obrysu
konštantnou hodnotou. V prípade Fourierovho radu sa to
prejaví vynásobením všetkých členov radu danou konštantou.
Tým pádom predelením celého radu jedným z jeho členov
dosiahneme normalizáciu pre veľkosť. Môže byť
dokázané, že v prípade prechodu obrysom proti smeru
hodinových ručičiek a disjunktnej kontúry, koeficient 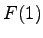 bude stále najväčší. Normalizácia v tomto prípade znamená
predelenie každého prvku
bude stále najväčší. Normalizácia v tomto prípade znamená
predelenie každého prvku 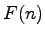 magnitúdou
magnitúdou 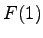 .
Vzniknuté koeficienty necháme v zlomkovom tvare.
.
Vzniknuté koeficienty necháme v zlomkovom tvare.
Normalizácia rotácie sa dá dosiahnuť nájdením koeficientov
dvoch prvkov s najväčšou magnitúdou. Následne nastavíme ich
fázový uhol na nulu. Ako bolo už v predchádzajúcom
spomenuté, 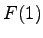 je koeficient najväčšej magnitúdy. Nech
je koeficient najväčšej magnitúdy. Nech
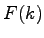 je koeficient druhej najväčšej magnitúdy. Tento koeficient
je koeficient druhej najväčšej magnitúdy. Tento koeficient
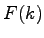 má násobnosť normalizácie (normalisation
multiplicity)
má násobnosť normalizácie (normalisation
multiplicity) 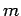 kde
kde 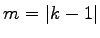 .
Teda podmienka, aby
.
Teda podmienka, aby 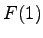 a
a 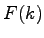 mali nulový fázový uhol môže
byť splnená
mali nulový fázový uhol môže
byť splnená 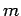 rôznymi orientáciami a kombináciami
štartovacích bodov. V prípade
rôznymi orientáciami a kombináciami
štartovacích bodov. V prípade 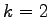 , orientácia a štartovací
bod sú definované jedinečným spôsobom.
, orientácia a štartovací
bod sú definované jedinečným spôsobom.
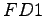 je málo efektívne pri
rekonštrukcii obrysu, preto sa zameriame na FD2.
je málo efektívne pri
rekonštrukcii obrysu, preto sa zameriame na FD2.
Pohyb bodu po hranici 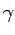 oblasti je popísaný
komplexnou funkciou
oblasti je popísaný
komplexnou funkciou
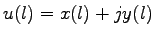 . FD2 je definované
ako:
. FD2 je definované
ako:
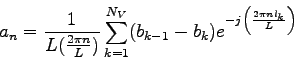 |
(3.42) |
pričom 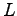 je absolútna dĺžka
je absolútna dĺžka 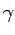 ;
;
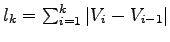 pre
pre 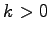 a
a 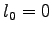 ;
a
;
a
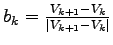 .
.
Nech 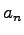 a
a 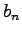 značia dva FD pre krivky
značia dva FD pre krivky 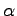 a
a 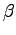 , ďalej sa predpokladá použitie
, ďalej sa predpokladá použitie 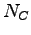 harmonických, potom metrika vzdialenosti je daná:
harmonických, potom metrika vzdialenosti je daná:
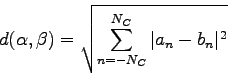 |
(3.43) |
Na to, aby sme vzali do úvahy zmenu merítka (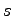 ), rotáciu
(
), rotáciu
(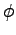 ) a
polohu štartovacieho bodu (
) a
polohu štartovacieho bodu (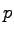 ), je potrebné minimalizovať metriku
vzdialenosti
), je potrebné minimalizovať metriku
vzdialenosti
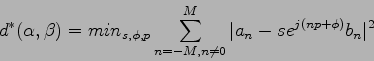 |
(3.44) |
pomocou nastavenia parametrov (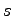 ,
,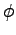 ,
,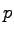 ). Toto je
výpočtovo náročná optimalizácia a tým pádom je FD2
nepraktické pre použitie v real-time spracovaní informácie,
hlavne vtedy keď počet obrázkov je veľký.
). Toto je
výpočtovo náročná optimalizácia a tým pádom je FD2
nepraktické pre použitie v real-time spracovaní informácie,
hlavne vtedy keď počet obrázkov je veľký.
Adrian Toth
2005-11-16