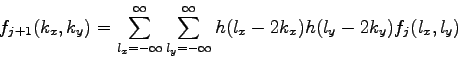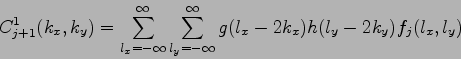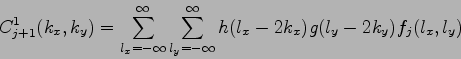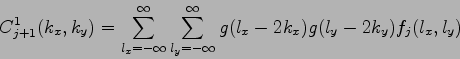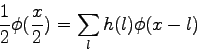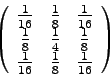Fourierova analýza poskytuje len globálnu informáciu, ktorá
nie je použiteľná na detekovanie kompaktných vzorov.
Gabor[19] zaviedol lokálnu aplikáciu
Fourierovej analýzy s posúvajúcim sa oknom, dôsledkom
čoho vytvoril akúsi časovo-frekvenčnú analýzu. Táto metóda je
aplikovateľná len vtedy, keď spojitý čas je nezávislý od
frekvencie[44]. Morlet-Grossmannova definícia spojitej wavelet transformácie pre jednorozmerný signál
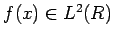
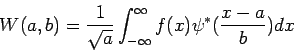 |
(3.12) |
pričom 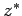 je komplexné združené číslo k
je komplexné združené číslo k 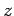 ,
, 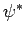 je
analyzujúci wavelet,
je
analyzujúci wavelet, 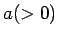 je scale parameter,
je scale parameter, 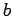 je
position parameter. Vlastnosti tejto transformácie sú
lineárnosť, kovariancia pri posune (
je
position parameter. Vlastnosti tejto transformácie sú
lineárnosť, kovariancia pri posune (
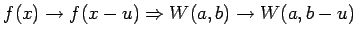 ), kovariancia pri
dilatácii (
), kovariancia pri
dilatácii (
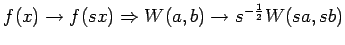 ). Posledná
vlastnosť robí wavelet transformáciu vhodnú pre hierarchické
štruktúry. Funguje ako matematický mikroskop, vlastnosti
transformácie nie sú závislé na zväčšení.
). Posledná
vlastnosť robí wavelet transformáciu vhodnú pre hierarchické
štruktúry. Funguje ako matematický mikroskop, vlastnosti
transformácie nie sú závislé na zväčšení.
Ako konkrétny príklad waveletu [52]
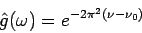 |
(3.13) |
je komplexný wavelet, môže byť rozložený na reálnu a
imaginárnu časť
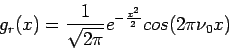 |
(3.14) |
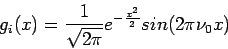 |
(3.15) |
pričom 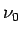 je konštanta. Kritérium prijateľnosti je
je konštanta. Kritérium prijateľnosti je
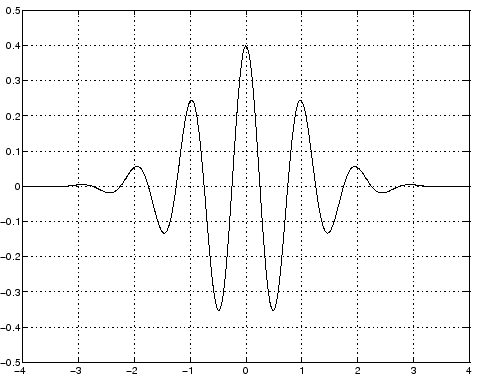
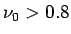 . Výstup takejto funkcie je uvedený na
obrázkoch 3.1, 3.2.
. Výstup takejto funkcie je uvedený na
obrázkoch 3.1, 3.2.
Obrázok:
Výstup reálnej časti
 |
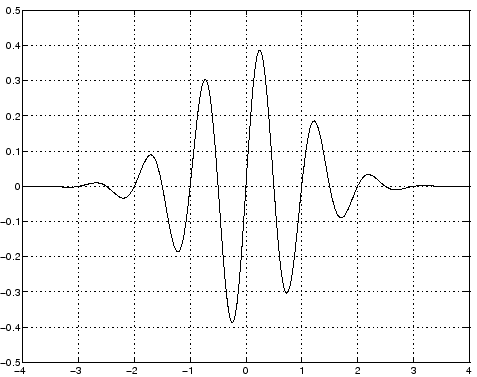
Obrázok:
Výstup imaginárnej časti
 |
Pri spracovaní obrazov vzorkovanie je robené v súlade so
všeobecne známou Shannonovou teorémou. Diskrétna wavelet
transformácia môže byť odvodená z tejto teorémy v prípade,
že spracovaný signál má obmedzenú frekvenciu. Digitálnu
analýzu získame diskretizáciou vzťahu 3.12.
Wavelet funkcia 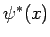 obyčajne nemá obmedzené
frekvenčné pásmo, tým pádom je potrebné potlačiť hodnoty
mimo pracovného intervalu, aby sme predišli rozmazaniu
signálu. Môžme pracovať vo Fourierovom priestore a
vypočítavať transformáciu postupne. Zredukovať počet
elementov v jednotlivých krokoch transformácie je možné len
pre wavelety s obmedzeným frekvenčným pásmom.
Multirezolučná analýza [37] vychádza z
množín generovaných interpoláciou pri rôznych rozlíšeniach.
Funkcia
obyčajne nemá obmedzené
frekvenčné pásmo, tým pádom je potrebné potlačiť hodnoty
mimo pracovného intervalu, aby sme predišli rozmazaniu
signálu. Môžme pracovať vo Fourierovom priestore a
vypočítavať transformáciu postupne. Zredukovať počet
elementov v jednotlivých krokoch transformácie je možné len
pre wavelety s obmedzeným frekvenčným pásmom.
Multirezolučná analýza [37] vychádza z
množín generovaných interpoláciou pri rôznych rozlíšeniach.
Funkcia 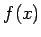 je premietnutá v každom kroku
je premietnutá v každom kroku 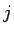 na podmnožinu
na podmnožinu
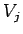 . Projekcia je definovaná súčinom prvkov
. Projekcia je definovaná súčinom prvkov 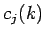 ,
,
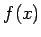 a
a 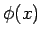 , pričom
, pričom
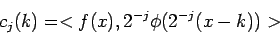 |
(3.16) |
Funkcia 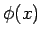 je škálovacia funkcia ktorá má vlastnosť
je škálovacia funkcia ktorá má vlastnosť
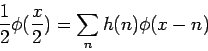 |
(3.17) |
alebo
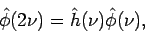 |
(3.18) |
kde 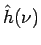 je Fourierova transformácia funkcie
je Fourierova transformácia funkcie
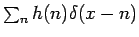 . Z toho vyplýva, že
. Z toho vyplýva, že
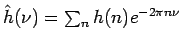 . Vzťah 3.17 nám
umožňuje vypočítať množinu
. Vzťah 3.17 nám
umožňuje vypočítať množinu 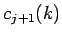 z množiny
z množiny
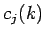 , a to pomocou vzťahu
, a to pomocou vzťahu
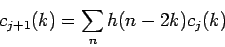 |
(3.19) |
V každom kroku je počet skalárnych súčinov delený dvomi.
Krok za krokom je signál vyhladzovaný a informácie sa
postupne strácajú. Znovuzískanie informácie je možné
použitím spätnej transformácie s príslušnou wavelet funkciou
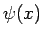 , ktorá má vhodné parametre - posun, dilatáciu.
, ktorá má vhodné parametre - posun, dilatáciu.
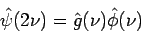 |
(3.20) |
Komplementárny podpriestor 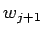 k
k 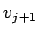 získame
výpočtom skalárnych súčinov
získame
výpočtom skalárnych súčinov
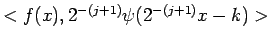 pomocou vzťahu
pomocou vzťahu
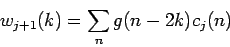 |
(3.21) |
Za účelom získania pôvodných dát [37]
využil vlastnosť ortogonálnych waveletov. V
[1] bola teória zovšeobecnená pre širšiu
triedu filtrov zavedením 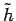 a
a 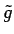 združených ku
združených ku
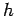 a
a 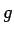 . Spätná transformácia (obnovenie) je potom daná
vzťahom
. Spätná transformácia (obnovenie) je potom daná
vzťahom
![\begin{displaymath}
c_{j}(k) = 2\sum_{l}[c_{j+1}(l)\tilde{h}(k+2l) +
w_{j+1}(l)\tilde{g}(k+2l)].
\end{displaymath}](img104.png) |
(3.22) |
Aby sme získali korektnú transformáciu musia byť splnené
podmienky 3.23(dealiasing) a
3.24(exact restoration).
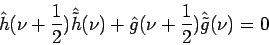 |
(3.23) |
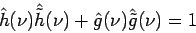 |
(3.24) |
Pri dekompozícii sa na funkciu aplikujú filtre 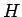 (nízke
frekvencie) a
(nízke
frekvencie) a 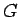 (vysoké frekvencie). Naopak, pri
rekonštrukcii aplikujeme filtre
(vysoké frekvencie). Naopak, pri
rekonštrukcii aplikujeme filtre 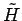 a
a 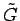 .
Ortogonálne wavelety zodpovedajú prípadu, keď
.
Ortogonálne wavelety zodpovedajú prípadu, keď
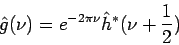 |
(3.25) |
a platí:
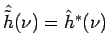 ,
,
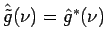 a je splnená
podmienka
a je splnená
podmienka
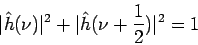 |
(3.26) |
Je jednoducho dokázateľné, že táto množina vyhovuje
podmienkam 3.23, 3.24. Biortogonálne
Daubechie-wavelety [1]
sú len konkrétnym príkladom ortogonálnych waveletov, platí
pre nich
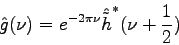 |
(3.27) |
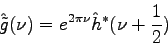 |
(3.28) |
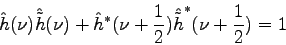 |
(3.29) |
Rozsiahla množina kompaktných waveletov môže byť odvodená.
Mnoho rôznych filtrov bolo navrhnutých, a bolo ukázané
[13], že voľba filtrov musí byť riadená
regularitou škálovania (scaling) a wavelet funkciami.
Algoritmus poskytuje pyramídu 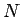 elementov, a jeho zložitosť
je proporcionálny k
elementov, a jeho zložitosť
je proporcionálny k 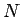 . Algoritmus pracujúci v 2D je
založený na dvoch premenných uprednostňujúcich smery
. Algoritmus pracujúci v 2D je
založený na dvoch premenných uprednostňujúcich smery 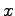 a
a
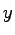 . Škálovacia funkcia je definovaná v tvare:
. Škálovacia funkcia je definovaná v tvare:
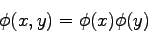 |
(3.30) |
Prechod z jedného rozlíšenia na ďalšie je možné pomocou
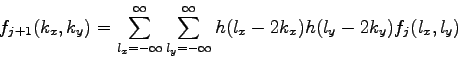 |
(3.31) |
Pomocou funkcií 3.32(vertikálny wavelet),
3.33(horizontálny
wavelet), 3.34(diagonálny wavelet)
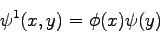 |
(3.32) |
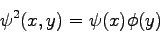 |
(3.33) |
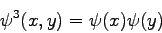 |
(3.34) |
získame transformáciu
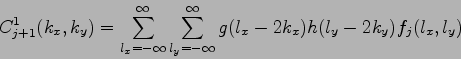 |
(3.35) |
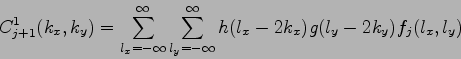 |
(3.36) |
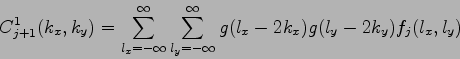 |
(3.37) |
pomocou ktorej rozdelíme obraz na tri časti[44],
viď obrázok 3.3.
Obrázok:
Reprezentácia obrazu po wavelet transformácii
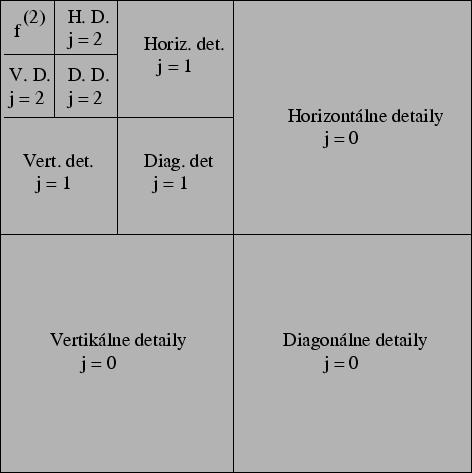 |
Transformácia pomocou waveletov môže byť chápaná ako
dekompozícia vo frekvenčnej oblasti s priestorovým
usporiadaním. Diskrétny prístup k waveletovej transformácii môže
byť implementovaný pomocou tzv. à trous
algoritmu. Tento algoritmus predpokladá, že 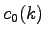 sú skalárnym súčinom funkcie
sú skalárnym súčinom funkcie 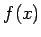 a škálovacej funkcie
a škálovacej funkcie
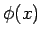 , zodpovedajúcej filtru v nižšom pásme, v bode
, zodpovedajúcej filtru v nižšom pásme, v bode 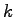 .
Prvá iterácia je potom vykonaná pri dvojnásobnom zväčšení,
pomocou ktorej získame
.
Prvá iterácia je potom vykonaná pri dvojnásobnom zväčšení,
pomocou ktorej získame 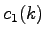 .
Rozdiel
.
Rozdiel
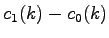 obsahuje množinu, ktorá je
charakteristická pre wavelet transformáciu pomocou funkcie
obsahuje množinu, ktorá je
charakteristická pre wavelet transformáciu pomocou funkcie
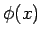 . Príslušný wavelet
. Príslušný wavelet 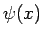 je potom definovaný
ako
je potom definovaný
ako
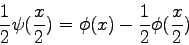 |
(3.38) |
Vzdialenosť medzi vzorkami pri hladine zväčšenia (i-1), a
konštantnom dvojnásobnom zväčšení medzi jednotlivými
hladinami je
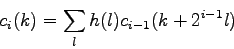 |
(3.39) |
a diskrétna wavelet transformácia
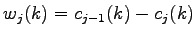 . Koeficienty
. Koeficienty 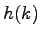 sú odvodené pomocou škálovacej
funkcie
sú odvodené pomocou škálovacej
funkcie 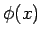 :
:
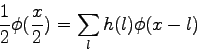 |
(3.40) |
Použijeme lineárnu interpoláciu funkcie
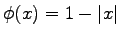 pre
pre 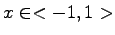 ,
, 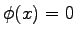 pre
pre
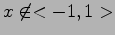 .
Interpoláciou získame funkciu
.
Interpoláciou získame funkciu 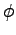 a príslušnú funkciu psi v
tvare uvedenom na obrázkoch 3.4,3.5
a príslušnú funkciu psi v
tvare uvedenom na obrázkoch 3.4,3.5
Obrázok:
Lineárna interpolácia funkcie 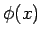
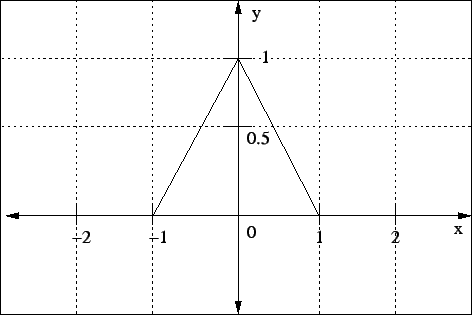 |
Obrázok:
Lineárna interpolácia funkcie 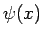
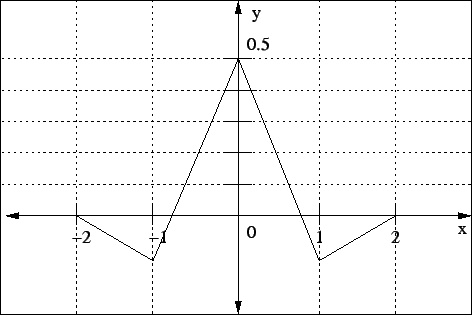 |
Vyššie popísaný algoritmus môže byť jednoducho rozšírený na
dvojrozmerný. Dostanem konvolučnú masku o veľkosti
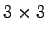 bodov pre wavelet spojený s lineárnou
interpoláciou. Koeficienty masky sú:
bodov pre wavelet spojený s lineárnou
interpoláciou. Koeficienty masky sú:
Na každej hladine 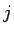 získame množinu hodnôt
získame množinu hodnôt 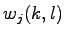 , ktorá
obsahuje rovnaký počet bodov ako samotný obrázok. V prípade,
že si zvolíme škálovaciu funkciu
, ktorá
obsahuje rovnaký počet bodov ako samotný obrázok. V prípade,
že si zvolíme škálovaciu funkciu 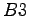 -spline, potom koeficienty
jednorozmernej masky budú v tvare
-spline, potom koeficienty
jednorozmernej masky budú v tvare
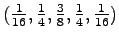 , a
dvojrozmerná maska bude vyzerať:
, a
dvojrozmerná maska bude vyzerať:
Vlastnosti textúr sú často získané prahovaním a morfologickou
transformáciou priestorovej a priestorovo-frekvenčnej
(spatial/spatial-frequency) časti
obrazu. Textúra môže byť reprezentovaná ako binárny vektor
príznakov, pričom každý prvok značí energiu v pomere ku
prahu v zodpovedajúcom s/s-f pásme. Každý s/s-f kanál je
reprezentovaný binárnym vektorom jednotkovej dĺžky
{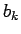 }.
{
}.
{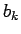 } predstavuje množinu elementárnych, lineárne nezávislých
vektorov, ktoré tvoria bázu pre binárny priestor textúr.
Vektory príznakov popisujúce vlastností textúr sú tvorené kombináciou
vektorov {
} predstavuje množinu elementárnych, lineárne nezávislých
vektorov, ktoré tvoria bázu pre binárny priestor textúr.
Vektory príznakov popisujúce vlastností textúr sú tvorené kombináciou
vektorov {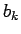 }. Proces extrakcie textúr z s/s-f pásma
prahovaním a morfologickou analýzou identifikuje regióny
textúr v rámci každého obrazu. Priestorová lokalizácia
jednotlivých textúr slúži ako sekundárne kritérium pri
určovaní podobnosti obrazov. Keďže väčšina algoritmov pre
extrakciu príznakov vlastností textúr zachová tvar regiónu, popis
tvaru regiónu môže slúžiť ako ďalšie kritérium podobnosti.
Gabor functions produkujú priestorovo-frekvenčnú
transformáciu obrazov s teoreticky malou mierou neurčitosti.
Dosahujú maximálne možné rozlíšenie v spektre s/s-f
vzťahmi
}. Proces extrakcie textúr z s/s-f pásma
prahovaním a morfologickou analýzou identifikuje regióny
textúr v rámci každého obrazu. Priestorová lokalizácia
jednotlivých textúr slúži ako sekundárne kritérium pri
určovaní podobnosti obrazov. Keďže väčšina algoritmov pre
extrakciu príznakov vlastností textúr zachová tvar regiónu, popis
tvaru regiónu môže slúžiť ako ďalšie kritérium podobnosti.
Gabor functions produkujú priestorovo-frekvenčnú
transformáciu obrazov s teoreticky malou mierou neurčitosti.
Dosahujú maximálne možné rozlíšenie v spektre s/s-f
vzťahmi
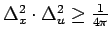 a
a
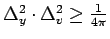 ,
pričom
,
pričom
![$[\Delta_{x}^{2},\Delta_{y}^{2}]$](img152.png) udáva priestorové
rozlíšenie a
udáva priestorové
rozlíšenie a
![$[\Delta_{u}^{2},\Delta_{v}^{2}]$](img153.png) je rozlíšenie
v priestorovo-frekvenčnej oblasti. K dobrým vlastnostiam pri
diskriminácii a segmentácii textúr je opodstatnenie Gabor-ových
filtrov podložené aj psychofyzikálnymi
experimentmi[6].
Adrian Toth
2005-11-16
je rozlíšenie
v priestorovo-frekvenčnej oblasti. K dobrým vlastnostiam pri
diskriminácii a segmentácii textúr je opodstatnenie Gabor-ových
filtrov podložené aj psychofyzikálnymi
experimentmi[6].
Adrian Toth
2005-11-16
![]() obyčajne nemá obmedzené
frekvenčné pásmo, tým pádom je potrebné potlačiť hodnoty
mimo pracovného intervalu, aby sme predišli rozmazaniu
signálu. Môžme pracovať vo Fourierovom priestore a
vypočítavať transformáciu postupne. Zredukovať počet
elementov v jednotlivých krokoch transformácie je možné len
pre wavelety s obmedzeným frekvenčným pásmom.
Multirezolučná analýza [37] vychádza z
množín generovaných interpoláciou pri rôznych rozlíšeniach.
Funkcia
obyčajne nemá obmedzené
frekvenčné pásmo, tým pádom je potrebné potlačiť hodnoty
mimo pracovného intervalu, aby sme predišli rozmazaniu
signálu. Môžme pracovať vo Fourierovom priestore a
vypočítavať transformáciu postupne. Zredukovať počet
elementov v jednotlivých krokoch transformácie je možné len
pre wavelety s obmedzeným frekvenčným pásmom.
Multirezolučná analýza [37] vychádza z
množín generovaných interpoláciou pri rôznych rozlíšeniach.
Funkcia ![]() je premietnutá v každom kroku
je premietnutá v každom kroku ![]() na podmnožinu
na podmnožinu
![]() . Projekcia je definovaná súčinom prvkov
. Projekcia je definovaná súčinom prvkov ![]() ,
,
![]() a
a ![]() , pričom
, pričom
 ,
,