Invarianty momentov (Moment invariants) sú vlastnosti
regiónov na binárnych
obrazoch, ktoré sú invariantné voči posunutiu, natočeniu a
zväčšeniu. Sú dobre použiteľné, pretože definujú jednoduchým
spôsobom vypočítanú množinu príznakov regiónu, ktoré môžu
byť použité pre klasifikáciu obrysov.
Moment invariantný voči posunutiu (
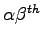 central) je definovaný ako
central) je definovaný ako
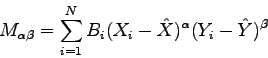 |
(3.55) |
pričom 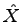 priemerná hodnota x
priemerná hodnota x
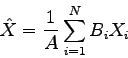 |
(3.56) |
a 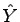 priemer súradníc y
priemer súradníc y
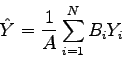 |
(3.57) |
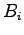 je binárna hodnota bodu na pozícii
je binárna hodnota bodu na pozícii 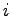 . Hodnota
A je počet bodov s hodnotou ``1''.
Ide vlastne o vypočítanie ťažiska plochy.
. Hodnota
A je počet bodov s hodnotou ``1''.
Ide vlastne o vypočítanie ťažiska plochy.
Z týchto momentov je možné vypočítať moment invariantný voči
zväčšeniu
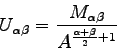 |
(3.58) |
V prípade, že časť obrazu sa zdvojnásobí, potom hodnota 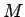 sa zväčši proporcionálne ku jej ploche. Menovateľ vzťahu
3.58 sa zväčší takým istým spôsobom ako čitateľ, preto
je činiteľ invariantný voči zväčšeniu.
sa zväčši proporcionálne ku jej ploche. Menovateľ vzťahu
3.58 sa zväčší takým istým spôsobom ako čitateľ, preto
je činiteľ invariantný voči zväčšeniu.
Pomocou
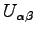 je možné odvodiť niektoré ďalšie momenty
invariantné voči rotácii.
je možné odvodiť niektoré ďalšie momenty
invariantné voči rotácii.
Adrian Toth
2005-11-16
![]() priemerná hodnota x
priemerná hodnota x
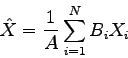
![]() priemer súradníc y
priemer súradníc y
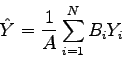
![]() je binárna hodnota bodu na pozícii
je binárna hodnota bodu na pozícii ![]() . Hodnota
A je počet bodov s hodnotou ``1''.
Ide vlastne o vypočítanie ťažiska plochy.
. Hodnota
A je počet bodov s hodnotou ``1''.
Ide vlastne o vypočítanie ťažiska plochy.