Dôvod, pre ktorý porovnávanie vlastností pre FD1 a FD2 je
výpočtovo náročná úloha je ten, že dĺžka susediacich 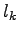 nie
je rovnaká. Ak zmeníme štartovací bod, celá
postupnosť
nie
je rovnaká. Ak zmeníme štartovací bod, celá
postupnosť 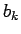 popisujúca obrys sa posunie.
popisujúca obrys sa posunie.
Tomuto nedostatku sa chceme vyhnúť definovaním hranice
zloženej vo všeobecnosti z 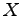 bodov (v [64]
konkrétne 4 body), s uniformnou dĺžkou. Nech
bodov (v [64]
konkrétne 4 body), s uniformnou dĺžkou. Nech
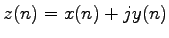 ,
,
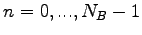 je postupnosť popisujúca obrys.
Potom MFD je definovaný ako Fourierova transformácia
je postupnosť popisujúca obrys.
Potom MFD je definovaný ako Fourierova transformácia 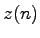 .
.
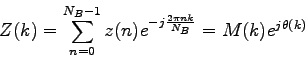 |
(3.45) |
pričom
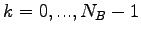 .
Ďalšom sú popísané vlastnosti MFD a návrh metriky, ktorá
je spoľahlivá a jednoducho vypočítateľná. Nech
.
Ďalšom sú popísané vlastnosti MFD a návrh metriky, ktorá
je spoľahlivá a jednoducho vypočítateľná. Nech 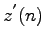 je
postupnosť popisujúca hranicu, ktorá bola získaná zo
je
postupnosť popisujúca hranicu, ktorá bola získaná zo 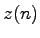 :
: 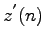 je
je 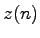 posunuté pomocou
posunuté pomocou 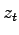 , natočené o uhol
, natočené o uhol 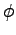 a zväčšené o
a zväčšené o
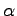 , so štartovacím bodom posunutým o
, so štartovacím bodom posunutým o 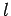 .
Explicitne vyjadrené, vzťah medzi
.
Explicitne vyjadrené, vzťah medzi 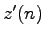 a
a 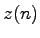 je daný
je daný
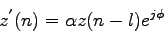 |
(3.46) |
Zodpovedajúce MFD 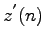 je
je
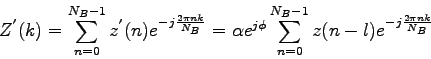 |
(3.47) |
Po označení 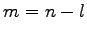 , dostaneme
, dostaneme
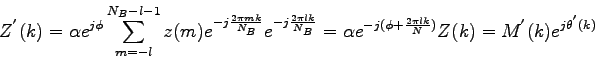 |
(3.48) |
pričom
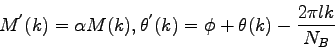 |
(3.49) |
Metrika vzdialenosti pre magnitúdu (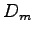 ) a fázu (
) a fázu (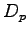 ) je
definovaná ako
) je
definovaná ako
![\begin{displaymath}
D_{m} = Var[ratio], D_{p} = Var[shift]
\end{displaymath}](img208.png) |
(3.50) |
kde jednotlivé symboly značia
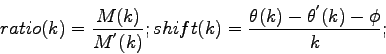 |
(3.51) |
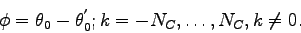 |
(3.52) |
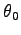 a
a
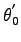 značia orientáciu hlavných
osí a sú definované ako
značia orientáciu hlavných
osí a sú definované ako
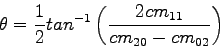 |
(3.53) |
kde 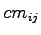 značí
značí 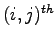 centrálny moment tvaru
(shape).
centrálny moment tvaru
(shape).
Globálna podobnosť tvarov je potom definovaná ako vážený
súčet
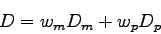 |
(3.54) |
kde 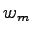 a
a 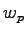 sú konštanty. Empiricky [64]
bolo zistené, že wm = 1 a wp = 0.1 budú vhodné pre väčšinu obrazov.
sú konštanty. Empiricky [64]
bolo zistené, že wm = 1 a wp = 0.1 budú vhodné pre väčšinu obrazov.
Adrian Toth
2005-11-16
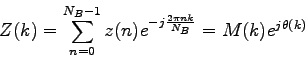
![]() je
je
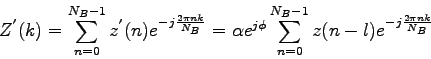
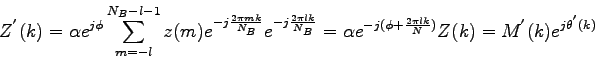
![]() ) a fázu (
) a fázu (![]() ) je
definovaná ako
) je
definovaná ako
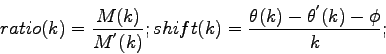
![]() značí
značí ![]() centrálny moment tvaru
(shape).
centrálny moment tvaru
(shape).