Textúry zodpovedajú vizuálnym vzorom, ktoré majú určitú
homogenitu, ktorá nie je spôsobená existenciou len jednej
farby alebo jasovej hodnoty v rámci
textúry[66]. Je to prirodzená vlastnosť
každého povrchu vrátane oblakov, stromov, vlasov, tkaniny a
pod. Obsahuje dôležitú informáciu o štrukturálnom
usporiadaní povrchu a jeho vzťahu k okolitému prostrediu
[59]. Z dôvodu dôležitosti a hlavne
použiteľnosti informácií o textúrach v Pattern Recognition a
Machine Vision, existuje pomerne rozsiahli výskum v tejto
oblasti.
Začiatkom 70-tých rokov Haralick[59] navrhol cooccurence matrix - kookurenčnú maticu. Tento prístup
spočíva v preskúmaní priestorovej závislosti hladín šedej.
Na zjednodušenie a uľahčenie práce s kookurenčnou maticou sa
hladiny šedej obyčajne zredukujú na menšie číslo, napr.
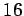 ,
, 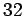 , a pod.
, a pod.
Nech 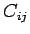 je ``konvenčná'' dvojrozmerná kookurenčná
matica zodpovedajúca kookurencii medzi hladinami šedej
je ``konvenčná'' dvojrozmerná kookurenčná
matica zodpovedajúca kookurencii medzi hladinami šedej
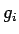 a
a 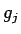 . Ak máme operátor pozície
. Ak máme operátor pozície 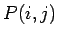 ,
maticu
,
maticu ![$A[i][j]$](img47.png) o veľkosti
o veľkosti 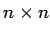 s prvkami
vyjadrujúcimi počet bodov s jasovou hodnotou
s prvkami
vyjadrujúcimi počet bodov s jasovou hodnotou ![$g[i]$](img49.png) vyskytujúcich sa v relatívnej pozícii
vyskytujúcich sa v relatívnej pozícii 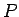 vzhľadom ku bodom
s jasovou hodnotou
vzhľadom ku bodom
s jasovou hodnotou ![$g[j]$](img51.png) . Matica
. Matica 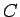 vznikne predelením
matice
vznikne predelením
matice 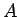 celkovým počtom bodov, ktoré spĺňajú podmienku
celkovým počtom bodov, ktoré spĺňajú podmienku
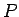 .
. ![$C[i][j]$](img53.png) reprezentuje pravdepodobnosť, že body
vyhovujúce podmienke
reprezentuje pravdepodobnosť, že body
vyhovujúce podmienke 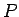 budú mať jasovú hodnotu
budú mať jasovú hodnotu
![$g[i],g[j]$](img54.png) . Matica
. Matica 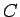 je kookurenčnou maticou definovanou
je kookurenčnou maticou definovanou
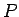 . Po získaní kookurenčnej matice - vypočítanej na základe
orientácie a vzdialenosti medzi bodmi - bolo možné získať
významné štatistické informácie.
. Po získaní kookurenčnej matice - vypočítanej na základe
orientácie a vzdialenosti medzi bodmi - bolo možné získať
významné štatistické informácie.
Subsections
Adrian Toth
2005-11-16