Extrakcia farebných príznakov je jedna z najčastejšie
používaných prístupov. Je to pomerne robustný prístup,
nezávislý od rozmerov, natočenia obrazu. Niektoré
reprezentatívne štúdie ohľadom vnímania farieb a možných
reprezentácií sú uvedené v [11][40].
Pre reprezentáciu farebných príznakov sa najčastejšie
používa histogram. Štatisticky znamená zjednotenú
pravdepodobnosť farebných hladín všetkých farebných kanálov
(zvyčajne R,G,B);
![\begin{displaymath}
h_{R,G,B}[r,g,b] = N . Prob \{R=r, G=g, B=b\}
\end{displaymath}](img5.png) |
(3.1) |
pričom R, G, B sú farebné zložky jednotlivých bodov, N
je počet bodov obrazu. Farebný histogram sa potom vypočíta
diskretizáciou farieb v rámci obrazu, a následným spočítaním
bodov každej farby. Keďže počet farieb je konečný, je
praktické pretransformovať histogram z funkcie troch
premenných na funkciu jednej premennej. Ak máme k dispozícii
RGB obraz, transformácia je daná vzťahom
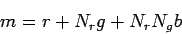 |
(3.2) |
kde 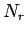 ,
,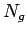 a
a 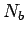 sú počty zásobníkov farieb pre
červenú, modrú a zelenú. Dostaneme
sú počty zásobníkov farieb pre
červenú, modrú a zelenú. Dostaneme
![\begin{displaymath}
h[m] = N . Prob \{M = m \}
\end{displaymath}](img10.png) |
(3.3) |
Existuje niekoľko metrík, pomocou ktorých
sa dá určiť miera podobnosti histogramov: euklidovská,
metrika L1 použitá v [70], metrika L2,
ktorá berie do úvahy podobnosť veľmi podobných ale nie identických
farieb[28]. Vzhľadom ku tomu, že vo väčšine prípadov
je histogram roztrúsený a citlivý na šum, v [35]
bol navrhnutý kumulovaný histogram (Cumulated
Color Histogram).
Popri farebnom histograme boli použité rôzne iné
reprezentácie farebných
príznakov. Na prekonanie kvantizačných efektov
použili [35] Color Moment - momenty farieb.
Matematickým základom tejto myšlienky je fakt, že každá
distribúcia farieb môže byť charakterizovaná jej momentmi.
Navyše bolo zistené, že väčšina podstatnej informácie je
sústredená v momentoch nižšieho rádu; v momentoch prvého
(priemer), druhého (rozptyl) a tretieho rádu (skewness).
Na určenie podobnosti bola použitá vážená Euklidovská vzdialenosť.
Na určenie podobnosti histogramov sa najčastejšie používa
metrika 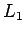 [70],
[70], 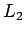 [45].
Ak histogram obrazu je definovaný ako vektor
[45].
Ak histogram obrazu je definovaný ako vektor
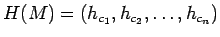 pričom
pričom 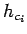 je počet bodov
s jasovou hodnotou
je počet bodov
s jasovou hodnotou 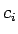 v obraze
v obraze 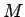 , a
, a 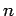 je počet
hladín. Bez straty
všeobecnosti si môžeme zadefinovať, že každý obraz má
je počet
hladín. Bez straty
všeobecnosti si môžeme zadefinovať, že každý obraz má 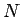 bodov, pričom
bodov, pričom
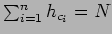 .
Vzdialenosť medzi dvomi farebnými histogramami
.
Vzdialenosť medzi dvomi farebnými histogramami 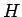 ,
, 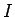 dané
metrikou
dané
metrikou 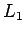 je definované ako
je definované ako
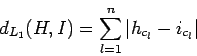 |
(3.4) |
Metrika zadefinovaná [45] využíva podobnosť
farieb v histograme. Usporiadame zásobníky tak, aby
susediace zodpovedali podobným farbám. Ak podobnosť farieb
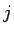 -tého a
-tého a 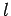 -tého zásobníka je
-tého zásobníka je 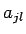 a symetrická
matica
a symetrická
matica 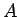 s prvkami
s prvkami 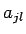 je kladne definitná, potom
je kladne definitná, potom
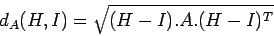 |
(3.5) |
definuje metriku 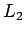 v priestore farebných histogramov.
v priestore farebných histogramov.
Color Sets - množina farieb, bola uvedená ako aproximácia
farebného histogramu a použitá na urýchlenie
prehľadávania veľkej množiny obrazov v
[67];
tento prístup spočíva v transformácii z (R,G,B) farebného
priestoru do priestoru uniformného z hľadiska vnímania
(X,Y,Z), napr. farebný priestor (H,S,V).
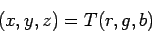 |
(3.6) |
Každej trojici 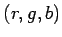 zodpovedá obraz
zodpovedá obraz 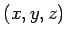 po
aplikovaní transformácie T.
Následne sa výkona kvantovanie farieb do M zásobníkov.
Nech
po
aplikovaní transformácie T.
Následne sa výkona kvantovanie farieb do M zásobníkov.
Nech 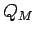 je funkcia, ktorá vykoná vektorové kvantovanie,
t.j. mapuje trojicu
je funkcia, ktorá vykoná vektorové kvantovanie,
t.j. mapuje trojicu 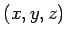 do jednej z
do jednej z 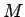 zásobníkov.
Potom
zásobníkov.
Potom
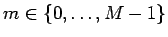 je index farby
je index farby 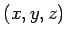 priradený funkciou
priradený funkciou 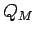 a je daný vzťahom
a je daný vzťahom
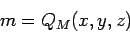 |
(3.7) |
Binárny farebný priestor 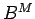 (Binary Color Space) je
(Binary Color Space) je
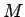 -rozmerný binárny priestor ktorý zodpovedá indexom
produkovaným pomocou
-rozmerný binárny priestor ktorý zodpovedá indexom
produkovaným pomocou 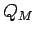 , pričom každý index
, pričom každý index 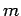 reprezentuje jednu os priestoru.
reprezentuje jednu os priestoru.
Napríklad nech 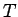 robí transformáciu medzi farebnými
priestormi
robí transformáciu medzi farebnými
priestormi 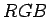 a
a 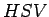 , a nech
, a nech 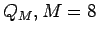 vektorovo kvantuje
priestor
vektorovo kvantuje
priestor 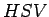 . Potom
. Potom 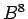 je osemrozmerný binárny
priestor, pričom každá os zodpovedá jednej farbe v
kvantovanom
je osemrozmerný binárny
priestor, pričom každá os zodpovedá jednej farbe v
kvantovanom 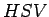 priestore.
Množina farieb (Color Set) je definovaná ako výber farieb z
kvantovaním rozdeleného farebného priestoru. Keďže vektory
popisujúce Color Set boli binárne bolo možné realizovať
efektívne a rýchle prehľadávanie. Vzťah farebného histogramu
a množín farieb bol preberaný v [68].
priestore.
Množina farieb (Color Set) je definovaná ako výber farieb z
kvantovaním rozdeleného farebného priestoru. Keďže vektory
popisujúce Color Set boli binárne bolo možné realizovať
efektívne a rýchle prehľadávanie. Vzťah farebného histogramu
a množín farieb bol preberaný v [68].
Adrian Toth
2005-11-16
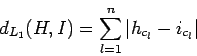
![]() -tého a
-tého a ![]() -tého zásobníka je
-tého zásobníka je ![]() a symetrická
matica
a symetrická
matica ![]() s prvkami
s prvkami ![]() je kladne definitná, potom
je kladne definitná, potom
![]() (Binary Color Space) je
(Binary Color Space) je
![]() -rozmerný binárny priestor ktorý zodpovedá indexom
produkovaným pomocou
-rozmerný binárny priestor ktorý zodpovedá indexom
produkovaným pomocou ![]() , pričom každý index
, pričom každý index ![]() reprezentuje jednu os priestoru.
reprezentuje jednu os priestoru.
![]() robí transformáciu medzi farebnými
priestormi
robí transformáciu medzi farebnými
priestormi ![]() a
a ![]() , a nech
, a nech ![]() vektorovo kvantuje
priestor
vektorovo kvantuje
priestor ![]() . Potom
. Potom ![]() je osemrozmerný binárny
priestor, pričom každá os zodpovedá jednej farbe v
kvantovanom
je osemrozmerný binárny
priestor, pričom každá os zodpovedá jednej farbe v
kvantovanom ![]() priestore.
Množina farieb (Color Set) je definovaná ako výber farieb z
kvantovaním rozdeleného farebného priestoru. Keďže vektory
popisujúce Color Set boli binárne bolo možné realizovať
efektívne a rýchle prehľadávanie. Vzťah farebného histogramu
a množín farieb bol preberaný v [68].
priestore.
Množina farieb (Color Set) je definovaná ako výber farieb z
kvantovaním rozdeleného farebného priestoru. Keďže vektory
popisujúce Color Set boli binárne bolo možné realizovať
efektívne a rýchle prehľadávanie. Vzťah farebného histogramu
a množín farieb bol preberaný v [68].