Na získanie informácií o textúrach sa najčastejšie používajú
transformácie, ktoré rozložia obrazový signál na harmonické
časti. Fourierova tranformácia (FT) je zovšeobecnením komplexného
Fourierovho radu.
Fourierov rad je rozšírením periodickej funkcie 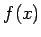 na
nekonečný súčet sínusov a kosínusov, využívajúc ortogonalitu
týchto funkcií. Výpočet a štúdium Fourierovho radu je známy
ako harmonická analýza funkcie, a je dobre použiteľná na
rozklad ľubovolnej periodickej funkcie na jednoduché časti,
ktoré sa dajú jednoducho riešiť, následne získať
riešenie celkového problému alebo jeho aproximáciu.
Zápis Fourierovho radu v komplexnom tvare je nasledovný
na
nekonečný súčet sínusov a kosínusov, využívajúc ortogonalitu
týchto funkcií. Výpočet a štúdium Fourierovho radu je známy
ako harmonická analýza funkcie, a je dobre použiteľná na
rozklad ľubovolnej periodickej funkcie na jednoduché časti,
ktoré sa dajú jednoducho riešiť, následne získať
riešenie celkového problému alebo jeho aproximáciu.
Zápis Fourierovho radu v komplexnom tvare je nasledovný
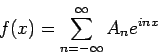 |
(3.8) |
pričom
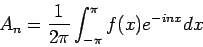 |
(3.9) |
Ak prepíšeme diskrétne 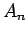 na spojité
na spojité 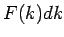 , t.j.
prejdeme z diskrétneho priestoru do spojitého, potom
sa dopracujeme k integrálu
, t.j.
prejdeme z diskrétneho priestoru do spojitého, potom
sa dopracujeme k integrálu
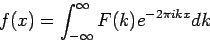 |
(3.10) |
Adrian Toth
2005-11-16