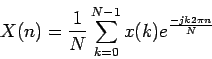Diskrétna Fourierova transformácia (DFT) je Fourierova
transformácia aplikovaná na rad diskrétnych komplexných
čísel. Predpokladajme rad komplexných čísel 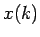 s
s 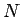 prvkami v tvare
prvkami v tvare
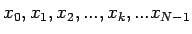 ,
pričom
,
pričom 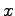 je komplexné číslo. Predpokladajme, že postupnosť
čísel je periodická, t.j.
je komplexné číslo. Predpokladajme, že postupnosť
čísel je periodická, t.j.
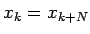 . Fourierova
transformácia
. Fourierova
transformácia 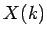 takéhoto radu bude mať
takéhoto radu bude mať 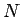 prvkov a bude
daná vzťahom
prvkov a bude
daná vzťahom
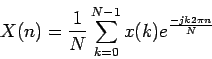 |
(3.11) |
pre 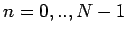 .
.
Fourierova transformácia ma široké spektrum použitia, na
druhej strane je použiteľná len pre stacionárne signály.
Adrian Toth
2005-11-16