Prírodou inšpirované algoritmy

Langtonove mravce

Podkapitoly:

Správanie niektorých mravcov
Kolektívne správanie
Prehľad appletov na webe
Applet pre Langtonove mravce
linky

C. Langton je objaviteľom prekvapivo jednoduchého automatu. ( Pozri applet.) Virtuálne mravce sa pohybujú po nekonečnej rovinnej mriežke, ktorej bunky môžu byť dvojakého druhu: biele a červené. Na počiatku je mravec v strede mriežky, a je mu daný nejaký smer (N, S, E, W ), ktorým sa bude pohybovať. Mravec sa posunie o jednu bunku vpred v smere podľa nasledujúceho pravidla: ak mravec príde na červenú bunku (alebo na bunku iného mravca, ak ich je viac), tak zmení jej farbu na bielu a otočí sa o 90 stupňov vpravo. Podobne, ak príde na bielu bunku, zmení ju na červenú a otočí sa vľavo o 90 stupňov. Na počiatku sú všetky bunky mriežky inicializované na bielu farbu. Mravec začne loziť a počas prvých 500 krokov sa periodicky vracia do jeho štartovacej bunky, pričom výsledný obrazec jeho lozenia je viac-menej symetricky. Je to i znázornené na tomto obrázku. V strede je vant pri návrate do svojho počiatočného stavu. Číslo vľavo hore udáva počet jeho prejdených krokov.

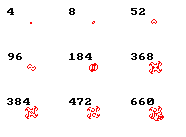
Neskôr, obrazce jeho lozenia sa stávajú trochu chaotické, až v istom okamihu sa náhle začne tvoriť diagonálny obrazec, nazývaný tiež diaľnica (highway). Na diaľnici mravec opakovane začne vytvárať obrazec pozostávajúci zo 104 krokov. Orientácia tejto diaľnice závisí jedine na počiatočnej orientácii mravca.

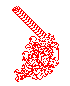
Ak začneme s inou počiatočnou konfiguráciou červených a bielych buniek, napr. porozhadzujeme do mriežky červené bunky, mravec ukončuje proces stavaním diaľnice. Dalo by sa povedať, že vo všeobecnosti nikto presne nevie akým spôsobom sa bude mravec správať. Jediným istým tvrdením je Kong-Cohenov teorém, ktorý vraví:

" Mravčia trajektória je nutne neohraničená a uniká z konečnej oblasti."

Vyskúšalo sa už niekoľko variácií na základné mravčie pravidlá. Napr., ak mravec lezie priamo vpred namiesto otočenia sa vpravo, tak vznikne horizontálna alebo vertikálna, dve bunky široká diaľnica. Iný návrh pravidiel počíta s tretím typom bunky, sivou bunkou, ktorá nikdy nemení svoju farbu. Pridané pravidlo potom znie, že ak mravec na svojom putovaní nájde sivú bunku, tak pokračuje nerušene v pohybe pôvodným smerom. V tomto modeli sa tiež vytvorí diaľnica.

Zovšeobecnené mravce

Zovšeobecnené mravce sú rozšírením Langtonových mravcov. Zovšeobecnený mravec je definovaný ako n stavov číslovaných od 0 po n-1 namiesto dvoch. V našich obrázkových reprezentáciách je n stavov reprezentovaných pomocou n rôznych farieb. Zovšeobecnené mravce navrhli G. Turk v Standforde a nezávisle na ňom L.Bunimovich a S.Troubetzkoy.

Zovšeobecnený mravec je popísaný pravidlovým n-bitovým reťazcom Sk={0,1}; k=0,1...,n-1

V každej iterácii mravec pokročí o jeden krok v danom smere, zistí si stav bunky na tejto pozícii a otočí vpravo ak k-ty bit v pravidlovom reťazci je 1 a vľavo v ostatných prípadoch. V tom istom okamihu, stav bunky zmení na (k+1)mod n, kde mod je operácia modulo. V tejto notácii je Langtonov mravec reprezentovaný reťazcom (1 0). Obrázok znázorňuje spávanie takto zovšeobecneného mravca.

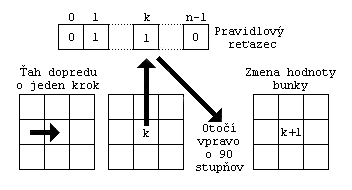
Pravidlové reťazce pozostávajúce zo samých jednotiek alebo núl sú triviálne, pretože mravec sa bude jednoducho otáčať v rovnakom smere (vpravo alebo resp. vľavo) v každom okamihu. Podobne, ak zinvertujeme všetky bity v pravidle, tak získame zrkadlovým obraz pôvodného obrazca. To možno vidieť v prípade mravca 5 (101) na nasledujúcom obrázku.

Je zaujímavé vyskúšať správanie niektorých netriviálnych zovšeobecnených mravcov. Zistíme, že vytvárajú isté všeobecne spoločné obrazce. Kvôli zjednodušeniu notácie a lepšej špecifikácii, budeme označovať mravce decimálnym číslom, ktoré bude odpovedať pravidlovému reťazcu, ak ho prevedieme do binárneho tvaru, napr. Langtonov mravec (1 0) bude v tejto notácii mravec 2. Ak nebude inak špecifikované, tak všetky bunky počiatočnej mriežky budú nastavené na nulu. Taktiež, mriežka bude v praxi konečnej veľkosti. Teda, budeme predpokladať, že ak mravec dosiahne okraj mriežky, tak tam ostane stáť. Každá simulácia bola prevedená s ohraničeným počtom krokov. Tieto výsledky preto treba chápať skôr za náznak ako za definitívny výsledok.

Jimm Propp vykonal simuláciu s niekoľkými zovšeobecnenými mravcami s pravidlovým reťazcom dĺžky 5 a 6, pričom našiel nejaké nové správania. Vo všeobecnosti, mravce s 5 bitovým pravidlovým reťazcom nevytvárajú dvojstranne symetrické obrazce, ale nové špirálovité správanie sa, ktoré začína mravcom 27. U 6 bitových pravidlových reťazcoch generujú mravce dvojstranne symetrické obrazce vtedy, ak číslo mravca je deliteľné troma.