Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Algoritmy IFS
Definícia IFS
IFS - systém iterujúcich funkcií je konečná množina kontraktorov w1, w2, ... , wn definovaných v určitom priestore. Nech (X,d) je úplný metrický priestor. Deterministickým systémom iterujúcich funkcií nazývame konečnú množinu spojitých funkcií F=(f1 , ... , fn) definovaných na X. Stochastickým systémom iterujúcich funkcií nazývame usporiadanú dvojicu (F,P) kde F je deterministickým systémom iterujúcich funkcií a P={p1 , ... , pn} , pi > 0 , p1 + ... + pn = 1 je množina pravdepodobností priradených každej funkcii z F.
Algoritmy IFS
Na generovanie obrazcov popísaných IFS poznáme dva typy algoritmov, sú to deterministický (applet) a stochastický (applet). Stochastický algoritmus je možné realizovať aj graficky, tzv. hrou chaosu (applet) K obom potrebujeme popis obrazca v nasledujúcom tvare, napr. pre Sierpinskeho trojuholník:
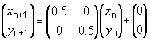
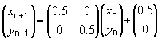
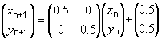
Deterministický algoritmus IFS.
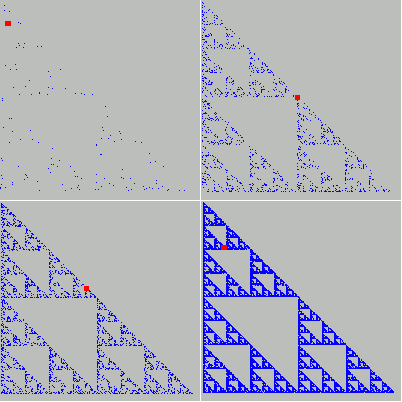
Uvedený deterministický algoritmus pracuje len s binárnymi hodnotami bodov. Na začiatku sa nainicializuje obrazové pole, minimálne jeden bod musí byť vysvietený. Ďalej sa prechádza celé obrazové pole rozmerov šírka x výška, na ktorom sa nad každým vysvieteným bodom aplikujú všetky funkcie (kontraktory) popisujúce daný útvar a pre každú funkciu sa prepočítajú súradnice nového vysvieteného bodu.
inicializuj( bool poleA[Vyška][Širka] ) // východzia množina
for ( i=0; i
{
vykresli( poleA );
for ( x=0; x
for ( y=0; y<Širka; y++ ) //stĺce
if ( poleA[x][y] == true )
for ( k=0; k
poleB[a[k]*x + b[k]*y + e[k]] // nová x súr.
[c[k]*x + d[k]*y + f[k]] = true; // nová y súr.
vymeň( poleA, poleB );
}
Na nasledujúcich obrázkoch môžeme vidieť prvé štyri iterácie Sierpinskeho trojuholníka v závislosti od inicializačnej množiny.

Stochastický algoritmus IFS
Stochastický algoritmus pracuje nad tým istým poľom, ako deterministický, len ku každej funkcii je priradená pravdepodobnostná hodnota výberu funkcie. Prvým krokom je vynulovanie celého poľa a určenie východzieho bodu. V ďalšom sa vyberie funkcia (kontraktor) podľa pravdepodobnosti výberu funkcie, ktorá určí súradnice nového bodu. Tento bod sa vysvieti a je zároveň vstupom pre ďalšiu iteráciu. Keďže sme pri inicializácii vyberali bod náhodne, tento bod a tiež niekoľko ďalších nie sú súčasťou výsledného obrázku, preto je vhodné vypustiť ich vykresľovanie.
inicializuj( x, y ); // náhodne alebo deterministicky napr. x=y=0
for ( i=0; i
{
vykresli( x, y );
k = VyberFunkcie( PočetFunkcií ); // náhodný výber
xx = a[k]*x + b[k]*y + e[k]; // nová x-ová súradnica
yy = c[k]*x + d[k]*y + f[k]; // nová y-ová súradnica
x = xx; y = yy;
}
Na nasledujúcom obrázku vidíme postupné generovanie Sierpinskeho trojuholníka pomocou stochastických IFS.