Prírodou inšpirované algoritmy

Farebný stroj katastrof

Podkapitoly:

Applet s rezom plochy lokálnych extrémov

Nižšie je uvedený applet, ktorý pomôže pochopiť, čo nazýva teória katastrôf "katastrofou". Predpokladajme, že pozorujeme systém, napr. bunku. Robíme s ňou pokusy. Vkladáme ju do rôznych roztokov reprezentujúcich rôzne prostredia. Cez zmeny hodnoty pH a teploty spoznávame ich vplyv na produkciu vybranej bielkoviny. Údaje, ktoré dostávame sú podivné, a sme sklamaní, lebo nerozumieme tomu, ako tieto dva faktory dokopy regulujú správanie sa bunky.

Pozrime si hru, ktorá napodobňuje túto situáciu (v istom zmysle je modelom chovania sa bunky): nižšie vidíme farebný štvorec. Kliknime a posúvajme kurzor myši vo vnútri oblasti označenej štvorcom. Súradnice kurzora simulujú spomenuté dva faktory a výsledná farba štvorca predstavuje intenzitu produkcie bielkoviny v bunke (zelená - vysoká, modrá - nízka). Teraz s ňou urobme zopár experimentov a skúsme ich výsledky zachytiť na papieri.

Applet ako čierna skrinka

Uvažujme teraz applet ako čiernu skrinku: má svoje vstupy (t.j. súradnice kurzora vo štvorci) i výstup (modrá až zelená farba štvorca). A hneď sme sa dostali k novému vzhľadu appletu: riadiacim poľom je ružový štvorec (v ňom treba posúvať ukazovateľ myši) a výstup sa objaví v obdĺžniku vpravo dole. Tento nový dizajn zobrazí čiernu skrinku medzi vstupom a výstupom. Našim cieľom je predstaviť si čo v sebe skrýva blackbox aby sme našli relácie medzi vstupom a výstupom.

• Vo väčšine systémov máme vložiť do čiernej skrinky funkciu: výstup = f (vstupy), danej kombinácii vstupov zodpovedá vždy rovnaký výsledok.
• V tomto prípade však dve výsledné hodnoty (modrá i zelená) zodpovedajú tomu istému vstupu (napr. bod v dolnej časti v strede). Výstup je závislý nielen na polohe kurzora ale aj na tom, v akom smere je posúvaný. Systém má pamäť, vnútorný stav a súradnice ukazovateľa spolu definujú výslednú farbu. Ďalším problémom je, že spojitá zmena vstupu nezapríčiní spojitú zmenu výstupu, ba naopak, pri niektorých kritických hodnotách sa prejavia významné skoky. Preto môžeme povedať, že systém je nelineárny, a spozorované správanie je kritický jav.

Teraz sa pokúsime experimentálne získané údaje znázorniť v 3D priestore.

• Vstupný priestor je dvojdimenzionálny (na obrázku ružový), je daný parametrami a a b.
• Výstupný priestor je 1D. Reprezentuje plynulý farebný prechod zo zelenej do modrej alebo opačne. Nazveme ho x.
• V 3D priestore (vstupný priestor x výstupný priestor) dostaneme po nanášaní údajov zdanlivé trhliny. Nad niektorými časťami vstupnej roviny sú dve údajové vrstvy. Ak posúvaný reprezentačný bod narazí na trhlinu (koniec vrstvy), skočí na druhú (najbližšiu).
• Nasledujúci obrázok (podľa L. Dujardin - so slovenským popisom) popíše situáciu, keď sú síce trhliny, ale je možnosť aj plynulej premeny modrej na zelenú.

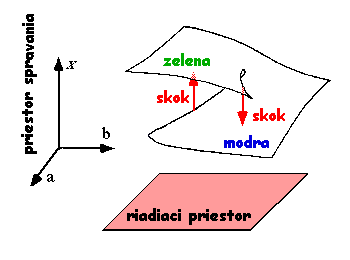
Aký povrchový útvar sa dá stotožniť s rozložením týchto dát? Matematici nemajú radi nespojitosti, nemajú radi rozštiepené povrchy. Uprednostňujú hladkosť. Ako nájdeme spojitosť v tomto rozštiepenom povrchu? A je vôbec tento povrch roztrhnutý? Môžeme si predstaviť plochu ako spojenie troch plôch: jedna ohnutá je vložená medzi dve čiastočne sa prekrývajúce skoro rovinné plochy. V matematike je to známe ako Riemann-Hugoniotov povrch alebo tiež hrot (vrchol). Teraz je už celá plocha hladká, pričom pridaný kus nevplýva na informácie v dátach, lebo je nedostupný pre systém.

Podrobnejšie sa matematickým opisom tejto plochy zaoberá samosatná podkapitola.

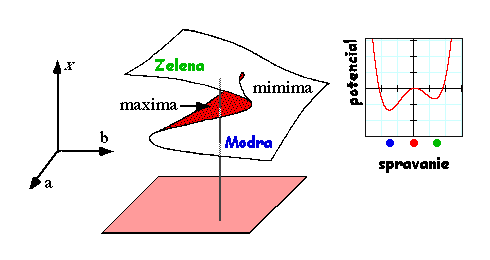
Potenciál V je funkciou x čo je riadené cez a a b ; píšeme to ako Va,b(x). Vieme, že systém má dve možné správania pre niektoré vstupy, preto hľadáme funkciu potenciálu Va,b(x) s dvoma minimami. Najjednoduchšia funkcia spĺňajúca tieto podmienky je polynóm štvrtého stupňa. Kanonický tvar, z ktorého sa dajú získať obe minimové funkcie je nasledovný: Va,b(x) = x4/4 - bx2/2 - ax. Môžeme si poznamenať, že Riemann-Hugoniotova plocha je množina bodov, v ktorých platí V'a,b(x) = 0, inými slovami množina miním a maxím potenciálu. Nasledujúci obrázok zosumarizuje doteraz získané informácie: dátová plocha v 3D priestore je množina miním potenciálovej funkcie. Graf ukazuje túto funkciu v špecifickom bode riadiaceho priestoru definovanom zvislou sivou priamkou. Trom priesečníkom priamky so skúmanou plochou zodpovedajú x-ové súradnice dvoch miním a jedného maxima krivky Va,b(x), ktorá je viditeľná na grafe. Vrstva prislúchajúca maximom (vyznačená červenou farbou na obrázku) je nedostupná systému (podľa L. Dujardin - so slovenským popisom)

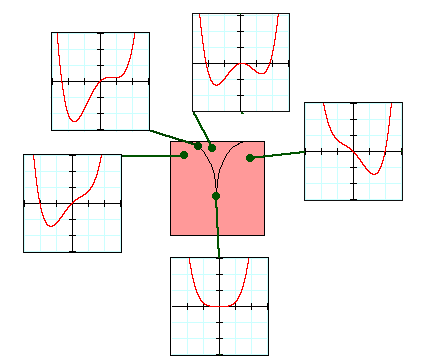
Teraz prejdime na ďalší obrázok (podľa L. Dujardin - nezmenený). V strede vidíme ružovú plochu reprezentujúcu riadiaci priestor. Okolo neho je umiestnených päť grafov, na ktorých vidíme tvar potenciálovej krivky pre vybrané body riadiacej plochy. Táto plocha je rozdelená na dve oblasti pomocou čiernej čiary, ktorá najprv rastie, potom sa obráti smerom nadol. Táto čiara sa volá bifurkačná krivka. Obsahuje kritické body plochy. Ostatné body sa nazývajú regulárne. V blízkosti regulárneho bodu krivka potenciálovej funkcie nemení svoj tvar, čo znamená, že počet jeho miním a maxím je konštantný. V kritických bodoch sa stretne jedno maximum s jedným minimom a obe sa stratia. Sú to body, v ktorých nastane skoková zmena v stave systému.

Jeden bod bifurkačnej krivky sa líši od ostatných: je to bod, v ktorom sa krivka otočí a začne klesať. V tomto bode sú dve minimá a maximum spojené. Zodpovedajúci potenciál je ploché minimum, ktorej rovnica je V = x4/4.

Detailnejšie experimenty s farebným strojom katastrof umožňuje applet.