Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Matematický opis
V teórii katastrôf sa pracuje s plochou lokálnych extrémov (PLE - equilibrium surface) reprezentujúcou povrch, ktorý je v určitých častiach špeciálne zakrivený. Pri pohybe nejakého telesa po tomto povrchu (vyvolanom napríklad pôsobiením gravitácie) dochádza na miestach špeciálneho zakrivenia k prepadnutiu telesa - nespojitému prechodu z jedného bodu plochy na druhé.
Najjednoduchšia potenciálová funkcia pre katastrofu typu hrot (cusp) má rovnicu:
y = x4/4 - ax2/2 - bx Premenné a a b
predstavujú súradné osi riadiacej plochy. Premenná a sa niekedy označuje ako faktor štiepenia a b ako normálový vektor. Premenná x je potom tzv. stavová premenná. Keď položíme deriváciu potenciálovej funkcie rovnú nule, tak dostaneme rovnicu plochy lokálnych extrémov:
y' = x3 - ax - b = 0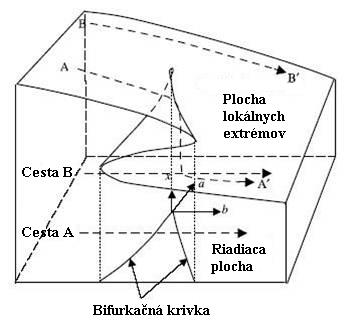
Plocha lokálnych extrémov
Pomocou parametrov a a b sa pohybujeme po v riadiacej ploche. Zmena môže byť hladká, alebo skoková. Z bodu B do bodu B' prejdeme plynulým znižovaním potenciálu. Pri pohybe z A do A' sa dostávame na okraj ohybu, kde malá modifikácia parametrov zapríčiňuje skok (katastrofu) na spodnú časť plochy. Čiara, ktorá vyznačuje okraje ohybu, sa nazýva bifurkačná krivka a dostaneme ju premietnutím prekrývajúcich sa častí plochy do riadiacej plochy.
Rovnicu bifurkačnej krivky dostaneme, keď diskriminant PLE položíme rovný nule.
Pre všobecný tvar rovnice tretieho rádu
a3z3 + a2z2 + a1z + a0 = 0sa diskriminant výpočita zo vzťahu:
D3 = (a12a22 - 4a02a23 - 4a13a3
+ 18a0a1a2a3
- 27a02a32) / a34Diskriminant pre PLE je potom:
D3 = 0*a 2 + 4*b*0 + 4*a31 + 18*b*a*0 - 27*b2kde prvý, druhý a štrvtý člen vypadne. Po porovnaní s nulou dostaneme výsledný tvar:
4a3 - 27b2 = 0A to je rovnica bifurkačnej krivky pre danú plochu.
Teraz hovorme o potenciálovej funkcii. Niektoré systémy sú známe riadením spotreby energie, alebo všeobecnejšie zmenšovaním potenciálu. Všimnime si, že nami rozoberaný systém (applet alebo syntéza bielkovín v bunke) je práve taký, ktorý minimalizuje potenciál. Čo teda systém robí? Prechádza do stavu, v ktorom vie najsilnejšie znížiť hodnotu potenciálu v závislosti od vstupov.
Musíme pripomenúť, že výskumník nepozná hodnotu každej vnútornej premennej, veľa z nich zostáva skrytých. Pozná iba vstupy a im zodpovedajúce výstupy. Hlavný prínos teórie katastrôf je v tom, že poukáže na to, že lokálny model systému znižujúceho potenciál (stratového systému) ignoruje veľmi vysoký počet vnútorných premenných. Komplexnosť lokálne spozorovaného správania je v skutočnosti určený niekoľkými výstupnými a riadiacimi parametrami.
Potenciál V je funkciou x čo je riadené cez a a b ; píšeme to ako Va,b(x). Vieme, že systém má dve možné správania pre niektoré vstupy, preto hľadáme funkciu potenciálu Va,b(x) s dvoma minimami. Najjednoduchšia funkcia spĺňajúca tieto podmienky je polynóm štvrtého stupňa. Kanonický tvar, z ktorého sa dajú získať obe minimové funkcie je nasledovný: Va,b(x) = x4/4 - bx2/2 - ax. Môžeme si poznamenať, že Riemann-Hugoniotova plocha je množina bodov, v ktorých platí V'a,b(x) = 0, inými slovami množina miním a maxím potenciálu.
Z týchto zdrojov sú prevzaté matematické vzorce a obrázok plochy (equilibrium surface) :
