Prírodou inšpirované algoritmy

Applet s rezom plochy lokálnych extrémov

Ovládanie appletu

Applet sa skladá z 3 častí. Prvou vľavo hore je riadiaca plocha (RP), v nej je vykreslená bifurkačná krivka. Kliknutím a pohybovaním myškou v tomto priestore nastavujeme parametre a a b. Tvorí ju bifurkačná krivka (BK), ktorá predstavuje hranicu, kde má potenciálová funkcia (PF) jedno alebo dve lokálne minimá. Taktiež môžeme parametre a, b nastaviť pomocou posuvných potenciometrov, či vstupných boxov, ktoré sú umiestnené pod RP. V druhej časti je jednoduchým spôsobom zobrazený priestorový pohľad na plochu lokálnych extrémov (PLE). Posuvnými potenciometrami, umiestenými pod touto plochou, môžeme zväčšiť či zmenšiť rozsah zobrazenia BK v RP (Zoom ab roviny) a PF (Zoom potenciálovej funkcie). V tretej časti je vykreslená PF a na nej krúžkom označené minimum potenciálu. Podklad je vyplnený farbou zmiešanou zo zložiek modrej a zelenej v závislosti od polohy určeného minima na x-ovej osi v grafe PF, hodnoty ktorých sa zobrazujú vpravo dole. Súčet týchto dvoch hodnôt tvorí číslo 255. Keď sa napríklad pohybujeme pod osou b v jej smere zľava doprava pribúda jas zelenej zložky (modrá ustupuje) pričom tento dej prebieha spojite. Ak to isté zopakujeme ale tentoraz nad osou b, zmena medzi farbami v určitom momente (pri prechode cez BK) nie je spojitá - ale skoková. Dochádza k javu, ktorý v teórii katastrôf nazývame katastrofa.

Ako applet funguje

Algoritmus využíva triedu Catastrophe.class, ktorej atribúty sú a, b a x_pos. Zároveň sú v nej metódy unfolding(x, a, b), ktorá slúži na výpočet funkčných hodnôt PF, equilibrium(x, a, b), ktorá slúži na výpočet funkčných hodnôt PLE a bifcurve(b) na výpočet a hodnôt BK. Špeciálnou metódou je minimize(), ktorá minimalizuje potenciálovú funkciu. Po použití tejto metódy sa v atribúte x_pos nachádza aktuálna x-ová súradnica minimalizovaného potenciálu. Z nej potom vieme vyjadriť zložky, ktoré budú tvoriť výslednú farbu farebného stroja katastrôf. A teda:

ktorá nadobúda hodnoty <0; 255> pričom x_pos je aktuálna xová súradnica minimalizovaného potenciálu, unf_zoom je koeficient zväčšenia PF a size je šírka grafu PF. Modrá zložka je doplnkom čísla 255 zelenou zložkou.

Bod číslo Green Blue 1 60 195 2 75 180 3 195 60 4 175 80 5 128 127 6 80 175 7 128 127

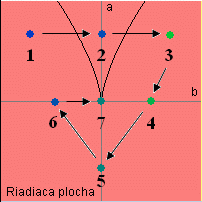
Hodnoty zložiek pri pohybe od bodu 1 k bodu 7 v smere šípok

Bod číslo Green Blue 1 60 195 2 180 75 3 195 60 4 175 80 5 128 127 6 80 175 7 128 127

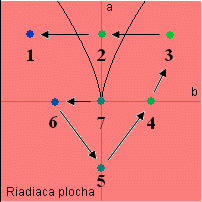
Hodnoty zložiek pri pohybe od bodu 7 k bodu 1 v smere šípok

Na obrázkoch sú naznačené kľúčové body riadiacej plochy a prechod nimi dvomi smermi. Vedľa každého obrázku sú v tabuľke zapísané číselné hodnoty farebných zložiek pre každý kľúčový bod. Po porovnaní oboch tabuliek vidíme, že sa líšia iba v bode 2.