Prírodou inšpirované algoritmy

Spring-block model

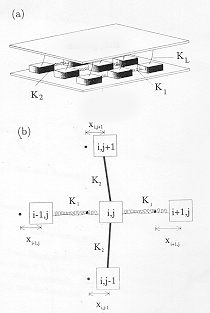
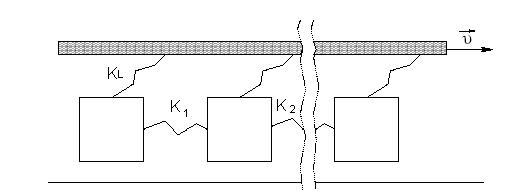
Burridge-Knopoffov spring-block model simulujúci zemetrasenia je dvojrozmerný dynamický model pozostávajúci z blokov na zafixovanej doske, ktoré sú spojené so svojimi najbližšími susedmi pomocou spojovacích pružín. Bloky sa po zafixovanej doske kĺžu vplyvom zaťažovacích síl. Každý blok je spojený s pohybujúcou sa doskou pomocou sklápacích pružín. Hlavná platňa predstavuje tektonickú dosku, sklápacie pružiny pôdu okolo tektonického zlomu a spojovacie pružiny reprezentujú interakciu medzi elementmi zlomu.

Silu pôsobiacu na každý blok môžme vyjadriť:

Fij=K1[2dxi,j-dx i-1,j-dx i+1,j]+K2[2dx i,j-dx i,j+1-dx i,j-1]+KLdx i,j

kde K1 a K2 sú horizontálne a vertikálne elastické konštanty spojovacích pružín a KL je elastická konštanta sklápacích pružín. Analógia zo zemetraseniami spočíva v spôsobe kĺzania blokov. Totiž ak na blok začne pôsobiť kritická sila, ten sa so svojej pozície skĺzne a vyvolá tým zaťaženie na svojich susedov prostredníctvom spojovacích pružín. Ak je zaťaženie susedov vyššie ako kritická hranica, dôjde k hromadnému sklzu. Ak skĺznutie prvého bloku vyvolá domino efekt, dochádza k situácii analogickej so zemetrasením.

Keďže tento BK model a jemu podobné modely sa riešia veľmi ťažko v dôsledku ich nelineárnosti, začali sa na ich riešenie využívať modely na princípe CA.

V ďalšej časti budú popísané tri základné typy CA modelov zemetrasení, ktoré zachycujú to najpodstatnejšie z množstva už existujúcich modelov.

Toto sú hlavné vlastnosti modelov, ktoré sa pri každom modeli líšia:

• Systém:
  • homogénny - všetky bloky majú rovnakú kritickú hranicu zaťaženia
  • heterogénny - kritická hranica u blokov závisí od rôznych vonkajších podmienok
• Sila pôsobiaca na systém:
  • globálna - zaťaženie pôsobiace na všetky bloky je konštantné
  • lokálna - blok, na ktorý pôsobí dané zaťaženie, je vyberaný náhodne
• Interakčné pravidlá medzi susediacimi bunkami - 4-susedstvo až 8-susedstvo
• Hranice modelu:
  • periodické - v systéme sa nič "nestráca", t.j. hocičo opúšťajúce jednu stranu systému vstupuje späť do systému na strane druhej
  • zafixované - informácia na okraji systému sa stráca
  • Niektoré modely kombinujú tieto dva prístupy, t.j. hranice sú periodické v horizontálnom smere a fixované vo vertikálnom
• Konzervatívnosť - tento dôležitý faktor popisuje veľkosť zaťaženia prenesenú zo skĺznutej bunky na jej susedov a veľkosť rozptýleného zaťaženia

BT model

Je to jeden z najskôr publikovaných modelov (1987). Model pozostáva z mriežky NxN, v ktorej má každá bunka náhodnú (celú) hodnotu z intervalu 0 až 4, kde hodnota 4 predstavuje kritickú hodnotu zaťaženia Zc.

Krok 1. Bunke Z(i,j), ktorá je náhodne vybratá, sa zvýši hodnota zaťaženia o 1 (lokálne rozrušenie)

Z(i,j) -> Z(i,j) +1

Krok 2. Ak zaťaženie bunky presiahne 4, hodnota zaťaženia sa zníži o 4 a pravidelne sa rozdistribuuje medzi 4 najbližších susedov. Ak tieto susedné bunky dosiahnu hodnotu Zc, proces sa opakuje. Trvá vlastne dovtedy, pokiaľ žiadna z buniek nemá hodnotu Zc, vtedy dôjde k návratu do kroku 1.

Z(i,j) -> Z(i,j) -4

Z(i± 1,j) -> Z(i± 1,j) +1

Z(i,j± 1) -> Z(i,j± 1) +1 pre Z(i,j)>Zc

O systéme platí, že:

• po čase sa dostane do kritického štádia
• je "konzervatívny", t.j. čo bunka stratí, jej susedia získajú
• model je nespojitý, keďže hodnoty buniek sú celé čísla
• v modeli sa využívajú fixované hranice

OFC model

OFC model sa od BT modelu líši tým, že je "nekonzervatívnou" verziou BK modelu. Druhým rozdielom je spojitosť OFC modelu, keďže bunky môžu nadobúdať reálne hodnoty medzi 0 a 1.

Pravidlá pre bunky Fij:

Pri inicializácii je bunkám priradená hodnota z intervalu 0 až 1. Pre bunky kde F(i,j)>Fc (Fc=1) sa aplikujú nasledovné operácie:

F(i± 1,j) -> F(i± 1,j) +a F(i,j)

F(i,j± 1) -> F(i,j± 1) +a F(i,j)

F(i,j) -> 0

kde a je faktor konzervatívnosti nadobúdajúci hodnoty medzi 0.25(konzervatívne) a 0 (úplne nekonzervatívne). Treba poznamenať, že tento faktor je veľmi citlivou premennou, ktorá dokáže podstatne zmeniť priebeh procesu. Toto pravidlo sa opakuje dovtedy, pokiaľ žiadna z buniek nedosahuje hodnoty Fc. Ak tento stav nastane, dochádza ku tzv. globálnemu rozrušeniu, pri ktorom sa hodnoty všetkých buniek zmenia podľa vzorca:

F=F+(Fc-Fmax)

Celý proces sa zopakuje.

Pre tento model takisto platí, že po určitom čase sa dostane do kritického štádia.

Mainov model

Tento model je veľmi podobný OFC modelu. Má rovnaké pravidlá pre interakciu medzi bunkami, rozdiel je len vo veľkosti faktoru konzervatívnosti b (b =4a ) 0 < b < 1.

F(i± 1,j) -> F(i± 1,j) +(b /4)*F(i,j)

F(i,j± 1) -> F(i,j± 1) +(b /4)*F(i,j)

F(i,j) -> 0

Ďalším rozdielom je konštantná zmena pri globálnom rozrušení a fakt, že v tomto modeli sa prihliada na termodynamické vlastnosti, čo značne zvyšuje komplikovanosť modelu.

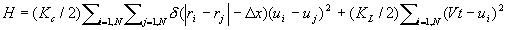
Prvý výraz predstavuje energiu spojovacích pružín, druhý energiu sklápacích pružín.