Prírodou inšpirované algoritmy

Zlatá špirála

Graf zlatej špirály súvisí s otáčajúcim sa zlatým obdĺžnikom. Špirálu s týmito vlastnosťami nazývame logaritmická špirála.

Dĺžky r sprievodičov sú úmerné uhlu , ktorý sprievodič zviera s pevnou osou.

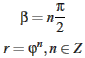
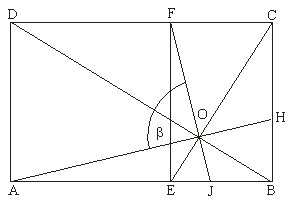
Logaritmickú špirálu môžeme približne zostrojiť pomocou štvrťkružníc vpísaných do vzniknutých štvorcov. Skutočná špirála sa nedotýka strán štvorcov, ale pretína ich pod veľmi malým uhlom. Uhol medzi dotyčnicou tejto krivky v jej ľubovoľnom bode a priamkou spájajúcou tento bod so stredom špirály je stály. Stred špirály O je priesečníkom uhlopriečok BD a CE, ktoré sú na seba kolmé. AH a FJ sa pretínajú v bode O a sú osami uhlov medzi BD a CE. Táto špirála má stále rovnako veľké zakrivenie, čo dosiahneme iba vtedy, pokiaľ nedodržiavame rovnakú vzdialenosť medzi závitmi (mení sa veľkosť sprievodiča), ale stále ich zväčšujeme a špirála veľmi rýchlo rastie. Logaritmická špirála sa zväčšuje, ale nemení tvar, rastie rovnako do dĺžky i do šírky. Či už ju zväčšíme na rozmery našej galaxie alebo zmenšíme na mikroskopické rozmery, tvar logaritmickej špirály sa nezmení. Tento tvar nachádzame u mnohých výtvorov prírody.