Prírodou inšpirované algoritmy

Zlatý obdĺžnik

Teraz si zvolíme obdĺžnik, ktorého strany sú v pomere 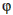, a nazveme tento obdĺžnik zlatým. Zlatý obdĺžnik má mnoho zaujímavých vlastností. Môžeme ho vpísať do štvorca tak, že všetky jeho vrcholy delia strany štvorca v zlatom pomere.

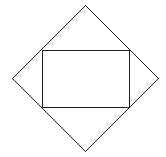
Ak oddelíme od zlatého obdĺžnika ABCD štvorec AEFD, bude ostávajúca časť opäť zlatým obdĺžnikom. Ak od obdĺžnika EBCF oddelíme štvorec GHCF, bude zbytok EBHG opäť zlatým obdĺžnikom atď.. Koeficient podobnosti zlatých obdĺžnikov je rovný . Platí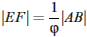

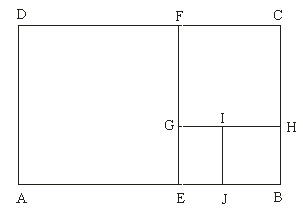
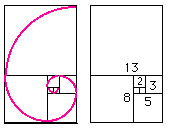
Vidíme, že poloha nasledujúcich zlatých obdĺžnikov sa mení, obdĺžniky sa otáčajú o pravý uhol. Body F, H, J, L..., vyznačujúce postupne zlaté rezy, ležia na zlatej špirále.

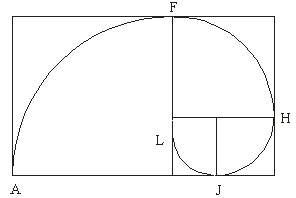
Je možné si všimnúť, že zlaté obdĺžniky sa otáčajú nielen v smere zmenšovania, ale i v smere rastu - z obdĺžnika EBCF môžeme dostať obdĺžnik ABCD a z toho opäť ďalšie, stále väčšie zlaté obdĺžniky. Za povšimnutie stojí prepojenie s Fibonacciho postupnosťou - keď totiž ukladáme k sebe štvorce so stranami o dĺžke rovnej členom postupnosti, dostávame zložený útvar - logaritmickú špirálu - nápadne sa podobajúci na Nautilovu mušľu (viď Zlatá špirála a Logaritmická špirála a jej rast)