Prírodou inšpirované algoritmy

Pickoverove biomorfy.

Úvod

Termín biomorf je odvodený z anglického výrazu biological morphologies (biologické tvary/útvary) a používa sa v oblasti umelého života vo viacerých významoch. V spojení Pickoverove biomorfy označuje útvary, ktoré sú podmnožinou fraktálov - obrazcov generovaných relatívne jednoduchými matematickými operáciami v komplexnej rovine. Ich podobnosť s primitívnymi formami života naznačuje, že príroda je formovaná na základe podobných jednoduchých zákonov.

Na prvý pohľad sa nám príroda okolo nás môže zdať chaotická. Keď sa však pozrieme lepšie, spozorujem isté zákonitosti. Už dlho sa vedci snažia odhaliť ich podstatu, nájsť ich presný formálny popis a postupne prichádzajú na to, že zdanlivo chaotický svet je v skutočnosti vysoko štruktúrovaný. Ukazuje sa, že pre zložité štruktúry v prírode a vo svete platí obmedzený počet jednoduchých pravidiel, ktoré sú však mnohorako kombinované.

Biomorfy ako fraktály

Jedným zo spôsobov, ako sa jednoduchým spôsobom zostavia komplikované štruktúry, je vytváranie geometrických útvarov iterovaním. Najznámejšie takto generované útvary - fraktály - sú Mandelbrotova množina Mandelbrotova množina a Juliove množiny.

Keď C. A. Pickover so svojim spolupracovníkom pripravoval program na preskúmanie iteračných metód získali obrázky podivne odlišné od Juliovych množín. Čoskoro zistili, že urobili v algoritme malú chybu, konkrétne v teste konvergencie (ohraničenosti) skúmaného bodu.

Vďaka spomínanej chybe v algoritme boli vygenerované obrázky oveľa zaujímavejšie a autori boli nimi "intelektuálne a esteticky uchvátení". Boli totiž zobrazené s množstvom detailov už pri malom počte iterácií N (narozdiel od "klasických" mandelbrotovských fraktálov), vo veľkej miere sa v nich vyskytovali zakrivené trojuholníkové tvary a čo bolo najdôležitejšie, pripomínali jednoduché živé organizmy. To podnietilo preskúmanie rôznych ďalších komplexných funkcií, zložitejších, obsahujúcich polynomiálne a transcendentné výrazy (v prípade mandelbrotovských množín sa pracuje iba s jednoduchou kvadratickou funkciou).

Nasledovali hodiny strávené pri obrazovke počítača a objavovanie nových "priestorov" a štruktúr pripomínajúcich tvary zo živej prírody. Práve kvôli tejto podobnosti si vyslúžili názov biomorfy (skratka z "biological morphologies").

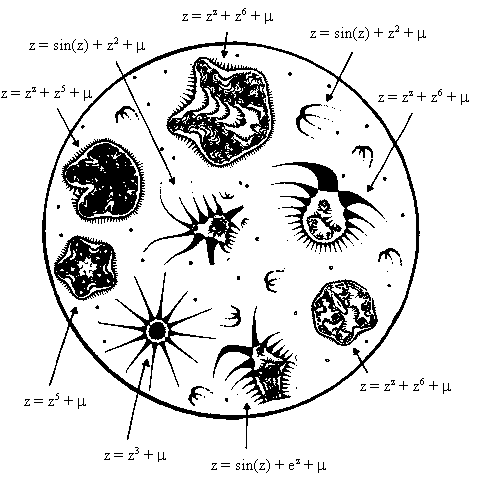
Pickoverove ZOO Biomorfy ((Pickover ,1990), (Pickover ,1986))

Vygenerované kreatúry sa vo väčšine podobajú na jednobunkové organizmy s brvami ("chĺpkami" zvonka bunkovej steny), napr. na protózu s rôznymi organelami. K iným nájdeme podobné kôrovce žijúce vo vode alebo hviezdice. Osovo súmerné útvary pripomínajú larvy niektorých morských živočíchov (z^z). 12-ramenná radiálne symetrická štruktúra (z^3) sa podobá na protózu s tenkými špicatými pseudopódmi. Iné biomorfy majú črty skeletov niektorých skamenelých organizmov. (Pickover ,1990) Mnohé pripomínajú rastliny. Niekoľko príkladov som umiestnil do galérie biomorfov.

Jednoduché demonštrácie

Po spustení appletu je v prvom okne vyobrazený biomorf pre funkciu exp(z)+sin(z) v základnom zväčšení, vyznačená oblasť z prvého obrázku je vyobrazená v prostrednom obrázku (odpovedá jej 8-násobné zväčšenie) a podobne aj vyznačená oblasť z prostredného obrázku je vykreslená v obrázku napravo (v 111-násobnom zväčšení). Tento applet ponúka možnosť vybrať si z niekoľkých príkladov (funkcií) a tiež zvoliť si farebný alebo čiernobiely režim zobrazovania.

Ovládanie: Po stlačení Reload (alebo po vybratí jednej z funkcií v rozbaľovacom zozname) je možné v prvom obrázku myšou vyznačiť ľubovoľnú oblasť, ktorú chceme priblížiť a daná oblasť sa zobrazí v okne napravo, pričom sa pod toto okno súčasne vypíše aj odpovedajúce zväčšenie. Aj v tomto okne je možné vybrať oblasť, pričom nový obrázok sa zobrazí v treťom okne. Ak sa vyznačí oblasť aj v treťom okne, obrázok sa presunie z tretieho do druhého okna a zväčšená oblasť sa zobrazí v treťom okne. Má zmysel približovať tie oblasti, v ktorých sa črtá hlbšia štruktúra. Zaškrtávacie tlačidlo Colors umožní vykresliť obrázok farebne alebo čiernobielo.

V druhom applete je možné si zvoliť vlastnú iteračnú funkciu:

Ovládanie: Applet umožňuje poskladať iteračnú funkciu zo základných funkcií, ktoré sa vyberú pomocou zaškrtávacích políčok. K iteračnej funkcii sa pripočítava komplexná konštanta u, ktorej hodnotu je možné zadať kliknutím do štvorca komplexnej roviny. Tvar aktuálne zvolenej iteračnej funkcie (aj s honotou u) je zobrazený v textovom poli. Dané nastavenia sa aplikujú stlačením Reload. Zaškrtávacie políčko Colors slúži na prepínanie medzi farebnou a čiernobielou verziou appletu a približovanie oblastí funguje na rovnakom princípe ako v prvom applete.

Význam farieb bodov v applete:

• ak bod konverguje (je "bounded"), zobrazí sa čiernou farbou (B)
• ak bod nekonverguje, čiže prekročí prahovú hodnotu po k krokoch, zobrazí sa v k-tej farbe (pri vyššom počte iterácií sa farby 1 - 16 cyklicky opakujú) - každá farba teda znamená 1 iteráciu naviac

Poznámky:

• Parametre appletov T (prahová hodnota testu divergencie) a N (počet iterácií) majú tieto hodnoty:
  • T = 8 pre oba applety
  • N sa približovaním zvyšuje u oboch appletov, počiatočná hodnota N v prvom applete závisí od funkcie, v druhom applete pre všetky funkcie N = 25.
  • Hranice výrezu komplexnej roviny, v ktorej sa zobrazuje prvý obrázok, v prvom applete tiež závisia od vybranej funkcie a v druhom sú konštantne nastavené na -5 a 5 (pre reálnu aj imaginárnu os).
  • Bližšie informácie o parametroch sú v podkapitole Algoritmy.
• Pri zväčšovaní sa fraktálová štruktúra nemusí vynárať plynule, ale "skokom" - je to v dôsledku toho, že ak sa dosiahne určitá hodnota priblíženia, zmení sa parameter N. Pre veľmi vysoké hodnoty priblíženia (okolo 10^13) sa štruktúra vytráca, čo súvisí s reprezentáciou číselných hodnôt v programe.

Význam biomorfov

Podobnosť biomorfov so skutočnými organizmami však nie je detailná, iba v základných rysoch. V prírode je stavba organizmov skúšaná a poznačená evolúciou, bojom o prežitie, kým biologické formy v komplexnom priestore sú generované iba iteráciou jednej funkcie bez akýchkoľvek vonkajších činiteľov a bez prvku náhody. Avšak zjavná podobnosť naznačuje, že živá príroda okolo nás bola (a je) formovaná podľa takých istých zákonitostí - je výsledkom opakovaného použitia jednoduchých dynamických pravidiel.

Biomorfy, podobne ako predhistorické mravce uviaznuté v jantári, nám hovoria o niekdajších primitívnych formách života. A ak sú takéto štruktúry vybudovateľné z jednoduchých matematických vzťahov, dá sa tušiť, že zložitejšie rovnice nám umožnia zobraziť v geometrickom priestore vyššie formy.