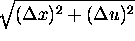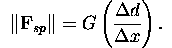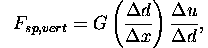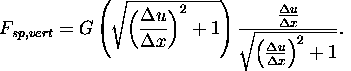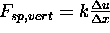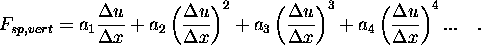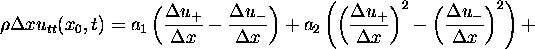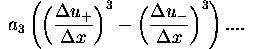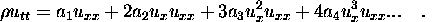|
Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
|
|
FPU vlnové rovniceFPU (Fermi, Pasta, Ulam) vlnové rovnicePokiaľ je struna v pokoji leží pozdĺž x-ovej osi. Keď
sa pohne, pohne sa iba v smere y-novej osi. Struna je modelovaná ako rad častíc zoradených pozdĺž x-ovej osi, nemôžu
sa pohybovať v smere x-ovej osi a sú od seba vo vzdialenosti 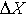 (objem častice je (objem častice je
r*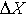 , kde , kde r je konštantná hustota struny). Každý pohyb častice v smere y je
namodelovaný s tým ohľadom, že dve susediace častice v strune sú spojené. Takto sú tiež modelované dlhé polymerické
molekuly.
u(x(0),t(0)) bude reprezentovať vertikálnu vzdialenosť (t.j. hodnotu y) v čase t(0) častice,
ktorej horizontálna poloha je x(0) a 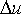 reprezentuje rozdiel vertikálnej vzdialenosti
medzi susednými časticami. Môžeme získať vzdialenosť medzi dvoma časticami reprezentuje rozdiel vertikálnej vzdialenosti
medzi susednými časticami. Môžeme získať vzdialenosť medzi dvoma časticami 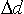 : :
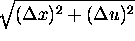
Hodnota sily na strunu je nejakou funkciou G a jej vzdialenosti. Môžeme ju normalizovať: 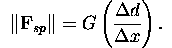
Keďže sa x-ová os je fixovaná stačí nám uvažovať iba vertikálnu zložku: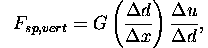
Čo môžeme reprezentovať ako funkciu: 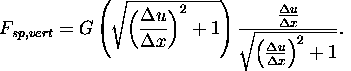
Ak je struna lineárna a má rovnovážnu dĺžku z=0, potom G(z)=kz, kde k je
kladná konštanta a teda: 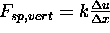
Pre z=0 a nelineárne struny, kde G(z) je analytická funkcia , ktorú za určitých
okolností môžeme upraviť na výraz: 
Ak je strunová sila analytickou funkciou 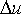 , namiesto analytickej
funkcie vzdialenosti môžeme písať: , namiesto analytickej
funkcie vzdialenosti môžeme písať: 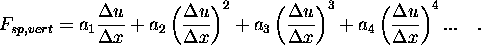
Ak definujeme: 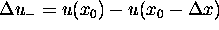 , , 
Potom: 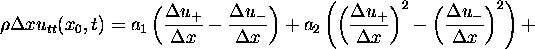 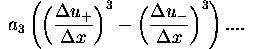
Ak 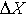 sa blíži k nule: sa blíži k nule: 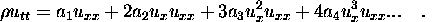
Pre náš model stačí uvažovať: 
Kde a(1)=k. Ak u(x) ostane malé, môžeme zanedbať vyššie mocniny: 
Táto rovnica simuluje schému (ii). Pre kubické rovnice (iii): 
Viac informácií nájdete v (Fermi, Pasta, Ulam, 1940).
|
|
Kontakt: Marek Bundzel |
(objem častice je
, kde
reprezentuje rozdiel vertikálnej vzdialenosti medzi susednými časticami. Môžeme získať vzdialenosť medzi dvoma časticami
:
, namiesto analytickej funkcie vzdialenosti môžeme písať:
,
sa blíži k nule: