Prírodou inšpirované algoritmy

Prechod z II do III

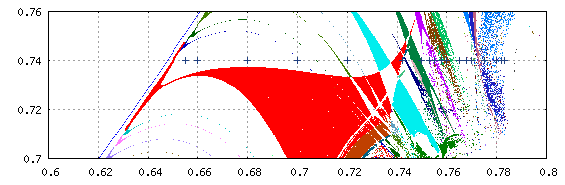Na obrázku hore sú vyznačené body, predstavujúce postupný prechod z oblasti II do III. Príslušné orbity sú uvedené na nasledujúcich 18. obrázkoch. Tabuľky parametrov obrázkov nájdete v diplomovej práci.

V nasledujúcej časti je vidieť postupné zväčšovanie invariantného cyklu (oblasť II), na ktorom po ustálení končia všetky body z bielej oblasti. Postupným približovaním k oblasti III sa charakter krivky stáva zložitejším.

a)	b)
c)	d)
e)	f)

V druhej časti (a a b) je možné pozorovať rozpad krivky invariantného cyklu na plôšky. Môžme to považovať za hranicu medzi oblasťami II a III. Oblasť kde sa tieto plôšky nachádzajú je veľmi úzka. Sú to oblasti, kde perióda atraktora je už veľmi vysoká.

a)	b)
c)	d)
e)	f)

Už zmena parametrov o jednu tisícinu zapríčiňuje zmenu atraktora z plôšok na podivný atraktor, tvorený čoraz zložitejšou spleťou čiar ako na obrázkoch dole - c), d), e) a f) (III). Táto sieť sa stáva zložitejšou až po hranicu s "nekonečnom". Presné určenie tejto hranice je veľmi obtiažne. Nie je to jasné (analyticky) tak, ako pri prechode z I do II. Na f) je invariantný cyklus nakreslený červenou farbou preto, aby vynikli čierne body "nekonečna", ktoré už naznačujú postupný prechod do oblasti IV. V tomto prípade skôr, či neskôr iterácia diverguje. Oblasť nie je celá čierna preto, lebo pre použitý počet iterácií nedôjde vždy k divergencii.

a)	b)
c)	d)
e)	f)

Celý prechod cez všetky obrázky si môžete pozrieť aj animovaným obrázkom vo formáte gif.