Prírodou inšpirované algoritmy

Priestoročasové obrazce a oblasti atraktorov

DDLab aj mvDDLab má dva druhy grafického výstupu simulácie, súvisiace tiež so spôsobom nazerania na dynamiku siete a druhom simulácie. Ide o zobrazovanie priestoročasových obrazcov pri doprednom behu siete, ktoré umožňuje skúmať miestnu dynamiku sústavy, a o kreslenie oblastí atrakcie atraktorov siete pri spätnom behu siete, ktoré poskytuje pohľad na celkovú dynamiku sústavy.

Dopredný beh simulácie znamená vytváranie časovej postupnosti stavov siete podľa jej stavov v predchádzajúcich okamihoch a podľa príslušných prepojení a prechodových pravidiel jednotlivých jej prvkov. To vlastne odpovedá "normálnemu" behu siete, jej normálnemu "životu" v diskrétnom čase. Bežnou grafickou reprezentáciou tohto behu je časová postupnosť bitových obrazcov predstavujúcich stavy siete v jednotlivých časových krokoch (priestoročasové obrazce). Program ponúka vykresľovanie tejto postupnosti ako animovaného obrazca (v 1D, 2D a 3D) alebo ako časovej postupnosti obrazcov v priestore (1D v 2D, 2D v 3D).

      

Na obrázku vľavo hore sú znázornené priestoročasové obrazce 50-prvkovej bool. siete. Bunky sú usporiadané v 1D priestore, ich časová postupnosť je v 2D. Modré štvorce predstavujú bunky v stave 1, biele sú bunky v stave 0. Jeden riadok predstavuje jeden diskrétny časový okamih. Obrázok vpravo hore zobrazuje priestoročasový obrazec celulárneho automatu LIFE. Celulárny automat má 3136 prvkov, ktoré sú usporiadané do štvorcovej matice 56x56. Obrazec na obrázku teda predstavuje len jeden (aktuálny) stav tejto siete. DDLab a mvDDLab však ponúka možnosť vykresliť aj stavy 2D siete ako časovú postupnosť v 3D priestore.

Dopredný beh nie je veľmi náročný na prostriedky počítača. Pamäť zaberá síce štruktúra siete, pravidlá a rôzne nastavenia, pri behu je však potrebné miesto už len pre súčasný a nasledujúci stav. Výpočtová náročnosť sa rovná náročnosti "vypočítavania" nasledujúceho stavu pomocou vyhľadávania v tabuľkách pravidiel. Programovo je veľkosť siete pri doprednom behu obmedzená číslom 65025 (255x255).

Spätný beh simulácie znamená vypočítavanie viacerých predchádzajúcich stavov k aktuálnemu, namiesto počítania nasledujúcich stavov. Tento postup spätne vybuduje celý podstrom predchodcov stavu v ktorom začne. Tento stav je koreňom podstromu a stavy bez predchodcov (tzv. rajské stavy) tvoria jeho listy. Úplný graf stavových prechodov (pre celý stavový priestor) sa vytvorí tak, že sa nájdu všetky stavy všetkých atraktorov siete, a k nim sa spätným behom vybudujú príslušné podstromy.

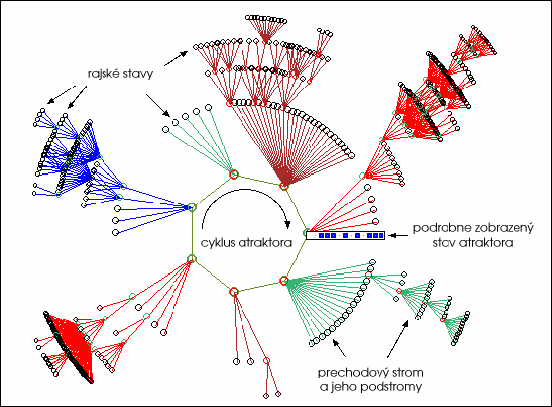
Nasledujúci obrázok zobrazuje graf stavových prechodov 13-prvkovej boolovskej siete. Graf odpovedá jednej z 15 oblastí atrakcie tejto siete. Nachádza sa v nej 604 stavov pospájaných orientovanými hranami podľa časovej následnosti (čas plynie smerom ku stredu grafu). 523 zo 604 stavov je rajských, tzn. že nemajú predchodcov. Dĺžka atraktora je 7 a jeden z jeho stavov je podrobne zobrazený ako bitový obrazec.

Nie je prekvapením, že tento spôsob činnosti je náročný na čas a pamäť. Program si musí pamätať všetkých predchodcov všetkých stavov na určitej úrovni grafu, tých bývajú bežne tisícky (veľkosť stavového priestoru rastie exponenciálne s veľkosťou siete), preto na začiatku umožňuje spätný beh len pre sieť s maximálne 31 prvkami. Toto obmedzenie sa dá obísť (napríklad pri nastavovaní prepojení) a využiť pre určité výnimočné prípady, pri ktorých je istota, že prostriedky počítača na ne vystačia. V opačnom prípade, keď si nie sme náročnosťou našich požiadaviek istí, program s najväčšou pravdepodobnosťou vyčerpá voľné prostriedky a spadne. Kvôli štúdiu oblastí atrakcie veľkých sietí však DDLab umožňuje vytváranie grafu stavových prechodov, napríklad, len od určitého počiatočného stavu alebo len do určitej úrovne atď.