Prírodou inšpirované algoritmy

Fylotaxia I.

Fibonacciho postupnosťami sa zaoberajú nielen matematici, ale aj botanici. Prečo? Listy, pokiaľ vyrastajú jednotlivo, sú na stonkách rozložené tak, že každý list vyrastá nad predchádzajúcim listom viac či menej posunutý o určitý uhol, ako je znázornené na obrázku

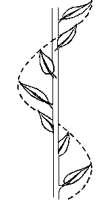
Tento uhol, ktorý je pre každú rastlinu charakteristický, vyjadrujú botanici v tvare zlomku, ktorý udáva, akú časť obvodu kružnice vytína. Čísla v čitateľoch aj menovateľoch zlomkov tvoria Fibonacciho postupnosť:

Zlatý rez sa tak nepriamo uplatňuje aj pri rozložení listov na osi rastliny. Fylotaxia (phylotaxis) je botanický termín pre postavenia listov na stonkách rastlín (viď taktiež Fylotaxia II.). V dolnej časti stonky sú listy staršie a väčšie, pri vrchole zasa mladšie a menšie. Všetky listy sú rovnomerne osvetľované, menšie netienia väčším, ktoré okrem toho majú ešte ďalšie kvetné lôžka. Zákonitosťami rozostavenia listov sa zaoberali, v 30.-40. rokoch minulého storočia francúzski bádatelia - bratia Louis a Antoine Bravais (Bravais & Bravais, 1838), a nemeckí morfológovia Karl Schimper(Schimper, 1831)(Schimper, 1836) a Alexander Braun (Braun, 1831). Títo botanici vybudovali celú náuku o postavení listov, ktorá k výkladom používa matematické formulácie.

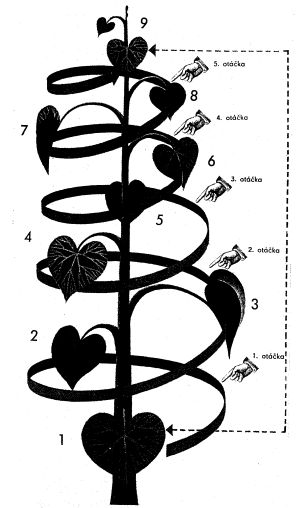
Listy sú postavené na stonke trojakým spôsobom, nás však bude zaujímať iba striedavé postavenie listov. Okolo stonky opisujeme skrutkovicu, ktorá vystupuje nahor podľa veku listov. Túto myslenú skrutkovicu nazývame genetická skrutkovica (v literatúre sa zvykne namiesto pojmu skrutkovica - 3D útvar - uvádzať aj nie celkom korektný pojem špirála, čo je však útvar 2D). Takto môžeme stanoviť, že listy sú postavené jednak do skrutkovice, pričom vždy určitý počet listov tvorí skupiny medzi dvoma listami stojacimi nad sebou a opakujúcimi sa pravidelne na celej stonke, a jednak tvoria určitý počet zvislých radov, v ktorých stoja listy vždy po určitom počte otáčok skrutkovice okolo osi. Teda dva susedné listy sú od seba vzdialené o určitú výškovú vzdialenosť dv a odchýlené o uhol - divergenciu di. Vzdialenosť je veličina premenlivá podľa šírky osi a strmosti genetickej skrutkovice, zatiaľčo divergencia je vždy stála a je možné ju vyjadriť zlomkom. Tento zlomok m/n, ktorý býva u celej rastliny rovnaký, udáva v menovateli počet listov v jednej skupine a v čitateli počet otáčok skrutkovice okolo stonky od prvého listu k nasledujúcemu, ktorý stojí priamo nad ním. Postavenie listov je možné znázorniť schematicky. Časť stonky pokladáme za pravidelný valec, ktorý je v podstate kužeľom, lebo sa smerom k vrcholu zužuje.

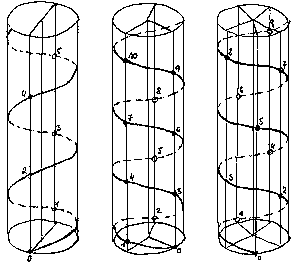
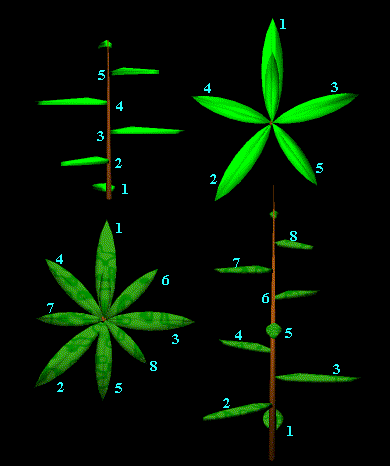
Na obrázku je schéma striedavého postavenia listov na stonke so zlomkom 1/2, ktorý nájdeme napr. na vetve lipy alebo vinnej révy - tu stojí vždy tretí list nad prvým, pričom celý cyklus obsahuje iba jediný obvod genetickej skrutkovice. Na vetve jelše alebo liesky tvorí genetická skrutkovica tiež jeden obvod, ale prechádza tri listy, aby došla k listu nad listom, z ktorého sme vyšli. Divergencia dvoch listov je 120°, všetky listy sú usporiadané do troch zvislých radov a zlomok je 1/3. U stromov napr. dub, višňa, topoľ, agát, vŕba či jabloň stoja listy striedavo v piatich radoch a genetická skrutkovica sa otočí okolo osi 2-krát, teda zlomok je 2/5. Menej časté je postavenie code>3/8, napr. ľan, redkvička, vavrín. Pre väčšiu názornosť uveďme diagramy postavenia listov podľa zlomkov 1/2, 1/3, 2/5.

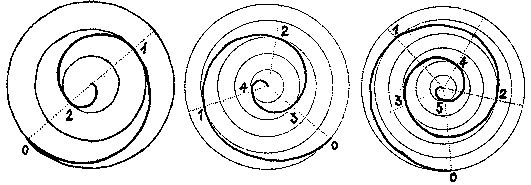
Presným pozorovaním a počítaním na rôznych druhoch rastlín bolo stanovené, že všetky divergencie môžeme zostaviť do radov:

alebo

alebo

u ktorých každý zlomok má v čitateli súčet čitateľov, v menovateli súčet menovateľov dvoch predchádzajúcich zlomkov. Jednotlivé divergencie sú potom konvergentné k hodnotám reťazcov

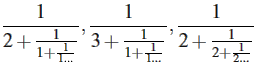
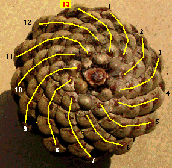
Sú to dokopy približné hodnoty podielu, keď obvod stonky rastliny rozdelíme zlatým rezom. Najčastejšie sú divergencie prvého rádu: podľa 1/2 má zostavené listy buk, brest, mnohé trávy; podľa 1/3 ostrica (druh trávy); podľa 2/5 väčšina našich stromov a krov; 3/8 ľan, ploník; podľa 8/21 sú usporiadané plodné šupiny v šuškách smreka a jedle; podľa 13/34 ihličie jedlí, šupiny v šuškách sosny čiernej. Kvety v úbore slnečnice sú usporiadané podľa 55/144.

Divergencie druhých rádov sú veľmi vzácne, napr. podľa 1/5 kvety v hlavici ďateliny, 2/7 v klase niektorých ostríc. Vzácne sa vyskytuje úkaz, že hneď druhý list stojí nad prvým, takže divergencia sa rovná nule, napr. u výhonkov hrušky. O príčinách zákonitého rozostavenia listov sú rôzne teórie. Alex Braun videl v skrutkovitom postavení listov uskutočnenie matematickej myšlienky v plánovitej stavbe rastlinného tela. Hanstein a neskôr Kerner vysvetľujú, že listy sa snažia zaujať také miesto, aby každý z nich mal dostatok miesta, vzduchu i svetla. V menovaní teórií by sa dalo pokračovať ďalej, je však nesporné, že rozostavenie listov závisí nielen na vnútorných podmienkach dedične fixovaných v každom rastlinnom druhu, ale taktiež na podmienkach vonkajších - majú často veľký vplyv na pomery vegetačného vrcholu. Pokiaľ vieme, že kvety dnešných rastlín vznikli premenou listov, nie je ťažké sa dovtípiť, že v skrutkovici by mali byť usporiadané i časti kvetu - kališné lístky, korunné lupienky, tyčinky a piestiky. V niektorých prípadoch je tomu skutočne tak. Skrutkovicu možno nájsť napríklad v kvete magnólie alebo slnečnice. Vo väčšine kvetov sa však závitnica vývinom tak stlačila, že vyzerá ako kruh, a okvetné lístky sú rozložené po jeho obvode. A čo šušky ihličnatých stromov? Keďže sú to zdrevnatené kvety či drevené klasy, ich šupiny by teda mali byť uložené na skrutkovici - a skutočně sú. Niektoré pravotočivé, iné ľavotočivé, všetky na jednom strome. Na rozdiel od listov sú však šupiny príliš pri sebe, divergencia je malá a genetická skrutkovica málo zjavná. V takom prípade vynikajú príkrejšie skrutkovice, ktoré nespájajú šupiny v genetickom poriadku, ale podľa šikmých paralelných radov, ktoré taktiež spájajú šupiny v zákonitom slede (viď ďalší obrázok).