Prírodou inšpirované algoritmy

Fylotaxia II.

Usporiadanie listov je na rôznych rastlinách rôzne. Na niektorých, ako napr. u hrachu, je každý list od svojho najbližšieho predchodcu pootočený o 180 stupňov. Stromy, ako jaseň alebo pagaštan konský, majú pre zmenu krížové usporiadanie, kde sa listy vyskytujú v pároch, ktoré sú pootočené od svojho predchodcu o 90 stupňov. U väčšiny kvitnúcich rastlín a ihličnanov rastú listy, prípadne ihličie, tým spôsobom, že od najstaršieho listu na stonke, postupne cez všetky listy, vieme vytvoriť základnú (fundamental) skrutkovnicu. Tak ako je zhruba rovnaký čas, pri objavením sa nového listu od svojho predchodcu, tak je rovnaký aj uhol a vzdialenosť nového púčiku.

Uhol medzi dvoma nasledujúcimi listami na stonke sa volá divergenčný uhol. Aby bol systém presne popísaný, musíme zaviesť ešte jeden parameter. Ak berieme do úvahy prierez rastliny, vhodná premenná je plastochronový pomer. To je pomer priečnych vzdialeností ku stredu listu. V rovnomernom systéme sa meria radiálnou expanziou vrcholu počas jedného plastochrónu. Keďže Turing namiesto prierezu uprednostňoval bočný pohľad, používal plastochrónovú vzdialenosť. Tá sa meria pozdĺž povrchu stonky. Okrem základnej skrutkovnice sa u veľa rastlín nachádza aj iná, prípadne iné. Tie sa volajú parastichné skrutkovnice. Je to vidieť na nasledujúcich dvoch obrázkoch. Listy sú číslované podľa sekvencie formovania.

Priečny rez pupencom rastliny mladej Prinus Pinei.

Priečny rez pupencom rastliny mladej Araucarie štíhlej.

Kontaktné parastichné čísla na prvom obrázku sú5 a 8 a na druhom 7 a 11. Sú to ilustrácie, ktoré sa objavujú vo veľa biologických prácach a je na nich zobrazený priečny prierez terminálneho pupenca rastliny (apical bud). Pri každom liste (na obr. znázornené ako očíslovaná oblasť), je vidieť vznik nie základnej skrutkovnice, ale hneď dvoch parastichných skrutkovníc. Keďže sú v kontakte, nazývajú sa kontaktné parastichné skrutkovnice. V dospelej rastline prechádzajú parastichné skrutkovnice daným listom, a potom nie jeho priamym nasledovníkom, ale listom o dva alebo tri listy za ním, resp. pred ním. Ak sú listy na stonke očíslované, podľa poradia ako vyrástli, je jednoznačne vidieť, že v parastichnej skrutkovnici bude rozdiel, medzi každými dvoma nasledujúcimi listami rovnaký. Prekvapujúce je, že v drvivej väčšine prípadov, tieto čísla, inak nazývané čísla poradia parastichných skrutkovníc, sú členmi Fibonacciho postupnosti, 1, 1, 2, 3, 4, 8, 13, 21.... . Čísla dvoch kontaktných parastichných skrutkovníc sú za sebou idúcimi členmi tejto postupnosti. Čiže ak k danému listu budeme pripočítavať vždy n-tý člen postupnosti, dostaneme prvú skrutkovnicu a ak n+1 člen postupnosti dostaneme ďalšiu, atď.

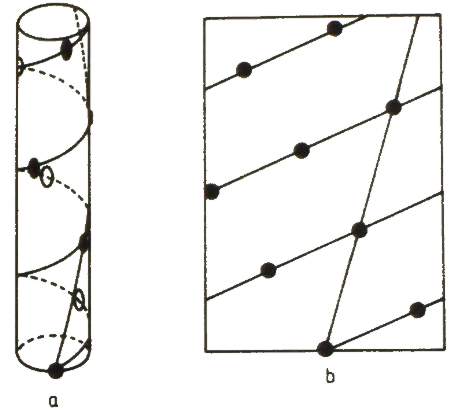
Ľavý obrázok je bočný pohľad na idealizovanú stonku. Vpravo je jej ekvivalent v rovine. Kontaktné parastichné čísla sú 1 a 2. Na obrázkoch je znázornená aj základná skrutkovnica, aj parastichná skrutkovnica 3 rádu.

Aj keď niekedy parastichné čísla nie sú priamo z Fibonnaciho postupnosti, často sú z postupnosti vytvorenej na základe podobných pravidiel. Napr. 1, 3, 4, 7... , 1, 4, 5, 9, ... alebo 2, 5, 7, 12, ... atď. V bočnom pohľade, ktorý používal Turing, sú kontaktné parastichné skrutkovnice menej zreteľné, ale na druhej strane je viditeľné, či sa na jednej úrovni nenachádza viac listov. Obyčajne je to len jeden, ale ak ich je náhodou viac, potom existuje aj viac základných skrutkovníc. Turing označil počet listov v jednej úrovni premenou J. Na nasledujúcom obrázku je J=1. Z toho vyplýva, že je len jedna základná skrutkovnica. Obrázok vpravo je ekvivalent ľavého obrázku v rovine, vytvoreného podľa postupu spomínaného vyššie.

Parastichná skrutkovnica nebude prechádzať listom na každej úrovni. Ak prechádza, každým n-tým listom, je n-tého stupňa. Turing nazval n parastichným číslom. Dovedna nájdeme na rastline nJ parastichných skrutkovníc. Všetky sú paralelné a každý list leží práve na jednej z nich. Tak môžeme rozdeliť listy na podmnožiny. Súbor mJ a nJ parastichných skrutkovníc, kde m a n sú vybraté tak, aby skrutkovnice z jednej z týchto dvoch skupín boli pravotočivé a druhé ľavotočivé, sa volá protiľahlý parastichný pár rádu (m, n). Pri každom strete týchto skrutkovníc sa nemusí nachádzať list, ale ak sa tam nachádza, tento pár sa nazýva viditeľný.