Prírodou inšpirované algoritmy

Margolusov biliárdový CA

Podkapitoly:

Applety

Biliardové celulárne automaty

Model biliardového automatu pozostáva z bodov v Karteziánskej sústave, z ktorých každý nadobúda hodnotu 0 alebo 1. To, či hodnota bunky bude 1 alebo 0 závisí na lokálnych prechodových pravidlách. Pre vytvorenie biliardového celulárneho automatu sú potrebné 4 rozličné stavy, ktoré bunka potrebuje pre reprezentáciu štyroch smerov gule, ďalej je potrebný jeden stav symbolizujúci prázdnu bunku a jeden stav pre odraz gule. Okrem toho musíme brať do úvahy aj 17 stavov susedných buniek. Preto Norman Margolus navrhol taký celulárny automat , ktoré využíva iný druh susedstva ako bolo zaužívané pri bežných CA (von Neumannove susedstvo). Toto susedstvo je známe ako Margolusove susedstvo. Margolus vyvinul sústavu CA, ktoré využívajú margolusove susedstvo s cieľom vytvoriť reverzibilný celulárny automat.

V jeho CA je bunka ohraničená striedaním plnej a bodkovanej čiary. Lokálne pravidlá sú aplikované na blok štyroch buniek ohraničených plnými a bodkovanými čiarami. Guľa(signál) je reprezentovaná dvojicou spoločne sa pohybujúcich buniek. Bunka sa rozdelila na 2x2 bloky a tým sa dosiahlo, že máme stavy pre 4 smery gule ako aj pre odrazy a aj pre prázdnu bunku.

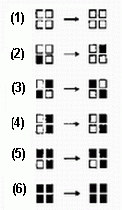
Každý 2x2 blok v karteziánskej sústave buniek berieme ako logické hradlo so 4 vstupmi (súčastný stav) a 4 výstupmi (nasledujúci stav). Tieto hradlá sú poprepájané úplne jednoznačným a jasným spôsobom na to, aby boli použité lokálne prechodové pravidla. Aby mohli byť použiteľné pravidlá pre bloky 2x2 striedame vytváranie blokov plnými čiarami v jednom kroku a prerušovanými čiarami v ďalšom kroku, tak ako je na predchádzajúcom obrázku. Na to, aby sa dosiahla v tomto systéme dynamika bolo potrebné do systému zaviesť nejaké prechodové pravidlá, ktoré sú znázornené na nasledujúcom obrázku. Prvé pravidlo reprezentuje prázdnu bunku.

Druhé pravidlo a jeho rotácie(v každom štvorčeku bloku 2x2) určujú prípad osamotenej "1", ktoré sa šíri priamo až do jedného zo štyroch rohov celulárneho priestoru.

Tretie pravidlo a jeho zrkadlový obraz rieši problém kolízie dvoch gúľ - ich odraz v kolmom smere.

Ďalšie štvrté pravidlo a jeho rotácia tvoria základný stavebný blok pre zrkadlá (odrazy), od ktorých sa gule odrážajú, tak ako je to na applete Stabilný prvok.

Piate pravidlo umožňuje odraz jedného signálu od zrkadla. Takisto aj toto pravidlo má svoje rotácie. Odraz gule od zrkadla je na nasledujúcom applete. Keďže druhé, štvrté a piate pravidlo majú štyri rotácie a pravidlo tretie má dve rotácie, potom celkový počet pravidiel spolu s prvým a šiestym pravidlom je 16.

Po každom odraze, ako je ukázané na predchádzajúcich štyroch appletoch sa signál oneskorí o dĺžku jedného bloku pozdĺž plochy zrkadla. Tým, že nastala zrážka sa guľa oproti svojej pôvodnej ceste (bez zrážky) oneskorí o dobu zrážky. Zrážkami gúľ alebo odrazom gúľ od zrkadiel môžeme realizovať nielen oneskorenie ale aj posun trajektórie oproti pôvodnej..