Prírodou inšpirované algoritmy

Model biliardového automatu

Model biliardového automatu

BBM je klasický mechanický systém, ktorý modeluje zmenu pozície v priestore a čase. Pozícia, rýchlosť a čas sú reálne premenné. Aby sme mohli uskutočniť digitálny výpočet, využijeme fakt, že celé čísla sú podmnožinou reálnych čísel. Vhodnou voľbou počiatočných podmienok môžeme dosiahnuť, že systém bude prejavovať svoju dynamiku v určitých časových krokoch. Ak máme dvojrozmerný priestor a niekde v tomto priestore máme nejaký bod, ktorý má v súčasnom časovom kroku hodnotu 1 v ďalšom časovom kroku môže mať hodnotu 0 alebo 1. Hodnota 1 sa pohybuje v priestore z miesta na miesto, ale ich počet (počet jednotiek v systéme) sa nemení. Nahliadnutie do pozadia BBM nám dáva nasledujúcu vetu:

Každé miesto, kde nastane zrážka v priestore konečného rozmeru sa javí ako boolovské logické hradlo. Na nasledujúcom obrázku máme túto vetu znázornenú graficky.

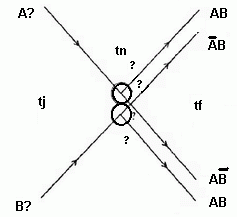
Vysvetlenie k obrázku:V bodoch A a B a v čase tj. v počiatočnom čase sa gule nachádzajú alebo nenachádzajú. Preto na obrázku sú body A a B označené ako A? a B?. Všetky vyznačené gule sa pohybujú rýchlosťou s. Ak sú obe gule v mieste A a B, tak sa zrazia v čase tn a následne sa odrazia a v čase tf sú gule v bodoch ako je vyznačené na obrázku. Na obidvoch stranách máme signály AB, čo je dané tým, že na jednej strane máme guľu A a signál od gule B. Na opačnej strane je to analogické, máme tam guľu B a signál od gule A. Pri zrážke gúľ sa gule odrazia opačným smerom, ale signály, ktoré gule nesú, prejdú cez miesto zrážky (bránu, hradlo) priamo (križovanie signálov). V prípade, že v čase tj máme len guľu A alebo B, tak v čase tn zrážka nenastane a pokračuje svojou cestou (aj signál, ktorý nesie). V čase t = tj je hodnota na pozícii A rovná 1, ak sa guľa nachádza na tejto pozícii, ináč je 0 (to isté platí aj pre B). Cesta gule predstavuje linku nesúcu signál. Zrkadlá (odrazy) zabezpečujú zakrivenia cesty gule.

Aby bolo možné použiť výstupy z jednej zrážky gúľ ako vstupy do druhej zrážkovej brány (hradla) potrebujeme veľmi precízne dohliadať na uhly zrážok a ich synchronizáciu, a tiež aj na rýchlosti jednotlivých gúľ. Toto jednoducho zabezpečíme obmedzovacími počiatočnými podmienkami. Každá guľa musí štartovať z bodu v mriežke Karteziánskej sústavy a pohybuje sa pozdĺž tejto mriežky v jednom zo štyroch povolených smerov. Ilustruje to nasledujúci obrázok.

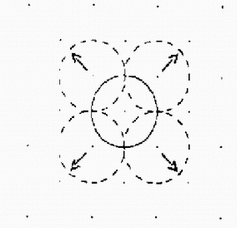
Všetky gule sa pohybujú rovnakou rýchlosťou. Čas za ktorý sa guľa presunie z jedného bodu mriežky do druhého nazývame časovou jednotkou. Rozstupy bodov v mriežke sú vybrané tak, aby sa gule odrážali a pohybovali len v mriežkach Karteziánskej sústavy.

Všetky gule sa odrážajú v pravom uhle a to tak, že jeden časový krok po zrážke sú gule stále v mriežke. Pevné odrazy (zrkadlá) sú situované tak, že gule ich zasiahnu ak sú v bode mriežky a po zrážke ostávajú v mriežke. Ilustrácia na ďalšom obrázku.

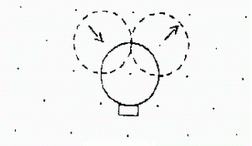
Konfigurácia odrazov na nasledujúcom obrázku rieši problém križovania dvoch signálov (netriviálneho). V prípade, že v mieste A sa guľa nachádza, v mieste B sa nenachádza (alebo opačne), táto guľa prejde do bodu na druhej strane a tým aj signál, ktorý nesie. Ak máme guľu v bode A aj v bode B, gule sa zrazia a prejdú cez konfiguráciu zrkadiel tak, že guľa B bude v mieste A a guľa B bude v mieste A, ale signály, ktoré tieto gule nesú prejdú do bodov B do B a A do A.

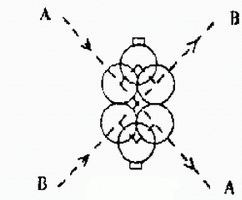
Odrazy a zrážky určujú možné cesty nasledujúcich signálov. Aby sa zabezpečilo, že všetky zrážky a odrazy boli len v pravom uhle, môžeme označiť všetky spojenia šípkami a obmedzíme počiatočné podmienky a medzispojenia tak, že guľa, ktorá je na danom spojení, sa bude pohybovať len v označenom smere.

Takýmto spôsobom môžu byť univerzálne brány pospájané a tak môžeme zostrojiť kvázi počítač. Výpočet môže bude zreťazený ako výkonná montážna linka, kde tok otázok sa mení na tok odpovedí. Reverzibilitu v tomto prípade zabezpečíme tak, že medzivýsledky môžu byť vymazané a nahradené predchádzajúcou odpoveďou systému. Pri spätnom chode (výpočte) sa môžeme zbaviť všetkých výsledkov, ktoré nie sú potrebné a kopírovať vstup.

Funkciu Fredkinovho biliardového modelu je možné si udskúšať v applete.