Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Mandelbrotova množina
Jedným zo symbolov teórie chaosu je Mandelbrotova množina (MM) - viď prvý obrázok, názorne ilustrujúca ako jednoduché (nelineárne) pravidlo je schopné generovať nesmierne zložité štruktúry.
Všetko sa to začalo už v období prvej svetovej vojny, keď Gaston Julia a Pierre Fatou študovali všeobecné vlastnosti mapovania jednoduchej funkcie komplexnej premennej x -> x2 + c, kde c je komplexná konštanta a z je komplexná premenná. Tie čísla z, pre ktoré iterácia zi+1 = zi2 + c nediverguje, tvoria Juliovu množinu (JM). JM-y vykazujú výraznú sebepodobnosť, pritom dynamika iteračného procesu a tým aj štruktúra JM vykazuje výrazné odlišnosti v závislosti na hodnote c.
Mandlebrot sa okolo roku 1970 vrátil k zabudnutým prácam Julia a Fatoua a študoval vlastnosti tej istej iteračnej formuly zi+1 = zi2 + c, lenže uvažoval c ako parameter a iteráciu začínal vždy hodnotou z0 = 0. Prvkami MM sú tie c v komplexnej rovine, pre ktoré absolútna hodnota čísla zi pri iterácii nerastie do nekonečna (prvý obrázok - body MM sú vyznačené čiernou farbou).
MM aj napriek tomu, že vzniká jednoduchým iterovaním komplexnej funkcie má výrazne fraktálový charakter. Aj pri mnohonásobnom zväčšení sa znova objavuje, hoci už nie celkom dokonalá kópia pôvodnej MM.

Mandelbrotova množina
Hoci nie je MM dokonale sebepodobná, keď pozorujeme jej rozhranie v postupne rastúcom zväčšení, opakovane sa v nej objavujú takmer identické štruktúry. MM je spojitá to znamená, že všetky jej časti sú pospájané tenkými vláknami. Vlákna vychádzajú aj z "bradavíc", pričom počet vetvení týchto vlákien je rovný perióde kmitov prislúchajúcich danej "bradavici".
V nasledujúcich appletoch je vidieť, že aj po mnohonásobnom zväčšení sa znova a znova objavuje aj keď nie úplne identická kópia pôvodnej MM (bielym štvorčekom je označená oblasť, ktorá je v ďalšom kroku 10 -krát zväčšená). Môžete si to vyskúšať aj sami. Po stlačení tlačidla reset si môžete sami zväčšovať časti MM.
Applety MM.
čiernobiela verzia appletu
farebná verzia appletu
Ovládanie appletov
Ovládanie appletov je veľmi jednoduché. Dalo by sa rozdeliť do troch krokov:
- Vykreslenie základnej mandelbrotovej množiny stlačením tlačidla "kresli" a vyznačenie oblasti, ktorá sa má zväčšiť.
- Vyznačenie oblasti na zväčšenie v druhom okne.
- Vyznačenie oblasti na zväčšenie v treťom okne. V ďalších krokoch sa oblasti na zväčšenie vyznačujú už len v treťom okne.
Počas zväčšovania je v prvom okne na hlavnej mandelbrotovej množine bielym krížom vyznačovaná poloha, kde sa užívateľ nachádza. V druhom okne je pre lepšiu orientáciu vyznačovaná štvorcom oblasť, ktorú si užívateľ zväčšil pri predchádzajúcom kroku. Pod oknami je informácia o aktuálnom zväčšení oproti hlavnej mandelbrotovej množine, ktorá je vykreslená v prvom okne.
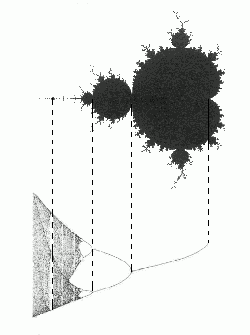
Vzťah MM a bifurkácií
Je veľmi zaujímavé sledovať vzťah MM a bifurkácií. Existuje medzi nimi určitá analógia. Ak pozorujeme dynamiku iterovania bodov MM na reálnej osi, zistíme, že závislosť ustálených hodnôt na reálnom c vytvára útvar pripomínajúci bifurkačný diagram logistickej rovnice (viď nasledujúci obrázok). Z oblasti kardioidy sa ustáli v jednom bode, z prvej bradavice kmitá s periódou 2, z druhej bradavice s periódou 4 až po oblasť chaosu. Na tomto obrázku je vidieť, že aj v miestach úplného chaosu sa objavujú okná bifurkácii, čiže orbit kmitá s nejakou konečnou periódou ( u najľavejšej čiarkovanej čiary je to perióda 3 ) a nie chaoticky.