Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Dynamika.
Hľadajme fixné body pre xn+1 = xn. Pre jednoduchosť indexy vynechajme.
f(x) = rx(1 - x) = x
x[1 - r(1 - x)] = x(1 - r + rx) = rx[x - (1 - r-1)] = 0
Fixné body, teda body riešenia sú x1(1) = 0 a x2(1) = 1 - r-1.
Na akom intervale hodnôt r sú tieto riešenia stabilné, sa môžeme presvedčiť pomocou už spomínanej podmienky |dxn+1/dxn| = |r(1-2xn)| < 1. Označme G(xn) = dxn+1/dxn, potom |G(xn)| < 1. Pre x1(1) = 0 : |G(0)| = |r| < 1 a riešenie v tomto bode je stabilné pre 0 < r < 1. V bode r = 1 riešenie nie je ani stabilné, ani nestabilné, je neutrálne.
Farebné krivky v grafoch reprezentujú prvé štyri iterácie f(x), f(f(x)), ..., f(f(f(f(x)))) logistickej rovnice, podobne ako na obrázku. .
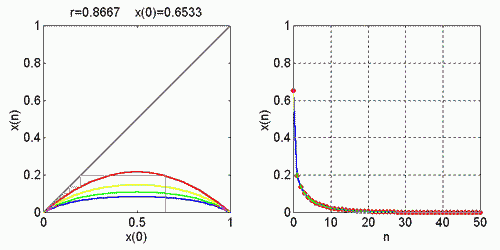
Pre x2(1) = 1 - r-1 : |G(1 - r-1)| = |2 - r| < 1 a riešenie je stabilné pre 1 < r < 3.
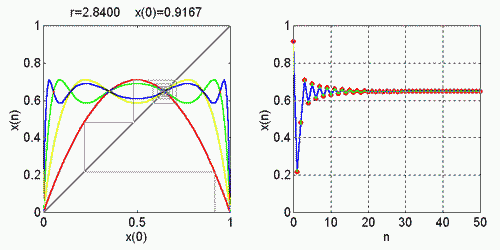
Čo sa stane, keď r >= 3 ? Pozrime sa na prípad, keď xn+2 = xn :
xn+2 = rxn+1(1-xn+1) = r[rxn(1-xn)][1-rxn(1-xn)] = r2xn(1-xn)(1-rxn+rxn2) = xnVzťah opäť upravíme a index n pre jednoduchosť nepíšeme:
f2(x) = f(f(x)) = r2x(1 - x)(1 - rx + rx2) = x
x{r2[1 - x(1 + r) + 2rx2 - rx3] - 1} = 0
x[-r3x3+2r3x2 - r2(1 + r)x + (r2 - 1)] = 0
-r3x[x - (1 - r-1)][x2 - (1 + r-1)x + r-1(1 + r-1)] = 0
Ako je z posledného vzťahu zrejmé, našli sme aj riešenia xn+1 = xn , lebo dva cykly s periódou 1 dávajú jeden cyklus s periódou 2. Pri xn+2 = xn riešenie sa neustáli na konštantnej hodnote, ale osciluje medzi dvoma hodnotami, ktoré sú dané koreňmi :
x(1) = 1 / 2{ (1 + r-1) + r-1[(r - 3)(r + 1)]1 / 2 }
x(2) = 1 / 2{ (1 + r-1) - r-1[(r - 3)(r + 1)]1 / 2 }
Korene sú reálne len pre r <= 3. Cyklus s periódou 2 ľahko nájdeme aj pomocou nasledovného vzťahu :
[ f2(x) - x ] / [f(x) - x ] = 0 .
Na nasledujúcom obrázku riešenia predstavujú body, kde žltá krivka pretína diagonálu a platí, že absolútna hodnota smernice dotyčnice v týchto bodoch je menšia ako 1.
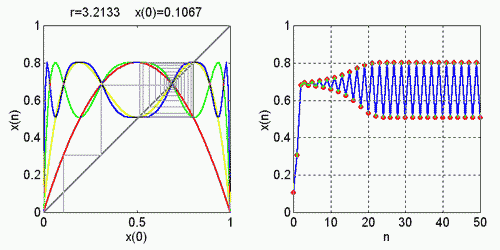
Cyklus s periódou 3, eliminovaním cyklu s periódou 1 hľadáme pomocou vzťahu :
f3(x) - x ] / [ f(x) - x ] = 0 Výsledkom podielu je polynóm šiesteho rádu, ktorého korene sú imaginárne a len pri r <= 1 + 81/2 sa objavujú reálne korene. Teda cyklus s periódou 3 vzniká pri r = 1 + 81/2= 3.8284... .
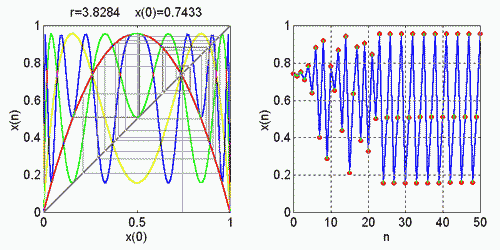
Cyklus s periódou 4 , eliminovaním cyklov s periódou 1 a 2 hľadáme pomocou vzťahu : [ f4(x) - x ] / [ f2(x) - x ] = 0 . Vznik cyklov s periódou 4 od r = 1 + 61/2 = 3.449489 :
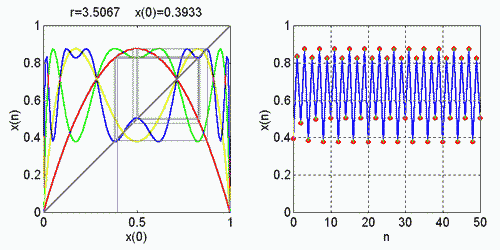
Cyklus s nekonečnou periódou, príklad na chaotický režim logistickej rovnice :
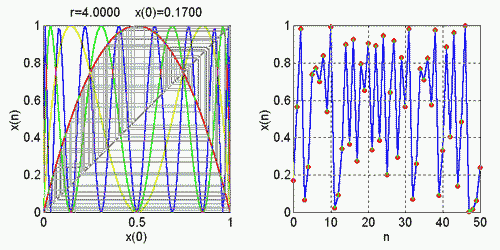
Logistická funkcia (presnejšie jej stav po nekonečnom počte iterácií) na intervale r = (0, 1) sa ustáli na hodnote 0, na intervale r = (1, 3) sa ustáli na hodnote 1 - 1/r. Pri r = 3 dochádza k oscilácii medzi dvoma hodnotami, dochádza k tzv. bifurkácii. Pri r = 1 + 61/2 docházda k ďalšiemu zdvojovaniu periódy, vznikajú cykly s peródou 4. Zvyšovaním r zdvojovanie periód pokračuje ďalej, vznikajú bifurkácie s periódou 2k , k = 3,4,5... na stále kratších intervaloch, až do hodnoty r = 3.5699457? čo je tzv. "akumulačný bod", kde začína chaotický režim - cyklus s nekonečnou periódou. Chaotický režim je ale v niektorých miestach prerušený úzkymi oknami cyklov s konečnou periódou. Napr. pri r = 1 + 81/2 = 3.8284... sa objavuje cyklus s periódou 3. Ďalší rast parametra r po tomto cykle je nasledovaný bifurkáciami s periódou 6,12.... Pomer medzi susediacimi intervalmi zdvojovania periód je stály, jeho veľkosť udáva Feigenbaumova konštanta , ktorá má hodnotu 4.66920160.
| n | cyklus 2n | rn |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 4 | 3.449490 |
| 3 | 8 | 3.544090 |
| 4 | 16 | 3.564407 |
| 5 | 32 | 3.568750 |
| 6 | 64 | 3.56969 |
| 7 | 128 | 3.56989 |
| 8 | 256 | 3.569934 |
| 9 | 512 | 3.569943 |
| 10 | 1024 | 3.5699451 |
| 11 | 2048 | 3.569945557 |
| inf. | akumulačný bod | 3.569945672 |
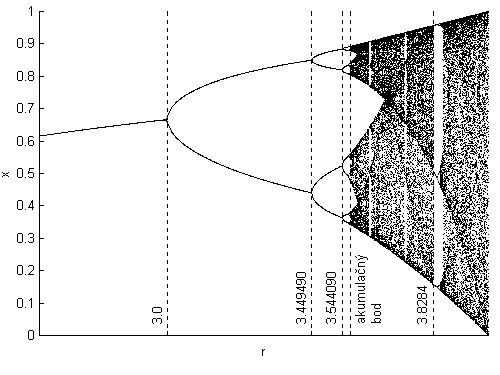
Stavy (hodnoty) sa po dostatočnom počte iterácií ustália na stálych hodnotách a (bez ohľadu na to, akú počiatočnú hodnotu sme volili) , vytvoria určitý obrazec, tzv. bifurkačný diagram . Čierne body predstavujú ustálené stavy, t.j. samotný bifurkačný diagram, fialové body predstavujú prechodný dej (prechodné stavy). Rôzne počiatočné podmienky dávajú rôzne prechodové deje. BD bol generovaný pre x0 = 0.999.
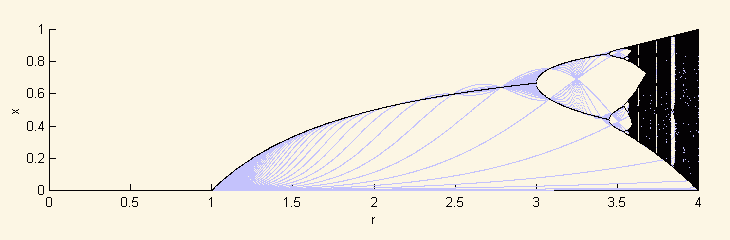
Bifukačný diagram vykazuje fraktálový charakter - kvázi-sebapodobnosť na rôznych úrovniach. Zväčšený výsek bifurkačného diagramu ukazuje značnú podobnosť s originálom, z ktorého samotný výsek pochádza. Jeho približnú fraktálovú dimenziu by sme mohli určiť experimentálnym spôsobom.
Chaotický režim logistickej rovnice vykazuje citlivosť na počiatočné podmienky, čo je charakteristické pre nelineárne systémy.
