Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Kolážová teoréma a komprimácia obrazu
Barnsleyho kolážová teoréma je matematickým východiskom pre fraktálové zakódovanie obrazu. Je určená vlastnosťami kontraktívneho iterujúceho systému a pre praktické účely je možné ju slovne interpretovať takto: Ak "približne pokryjeme množinu S obrazmi seba samej, ktoré dostaneme pomocou afinných transformácií, z ktorých sa skladá kontraktívny systém iterujúcich funkcií, potom atraktor tohto iterujúceho systému aproximuje obraz S. Napríklad obdĺžnik môžeme pokryť obrazmi seba samého v kontraktívnych afinných transformáciách w1, w2, w3 a w4 tak, že
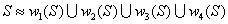
V zmysle Hutchinsonovej definície
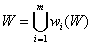
je konečná množina m kontraktívnych afinných transformácií približne zhodná s pôvodným obrazom. Takáto množina sa nazýva kolážou pôvodného obrazu.
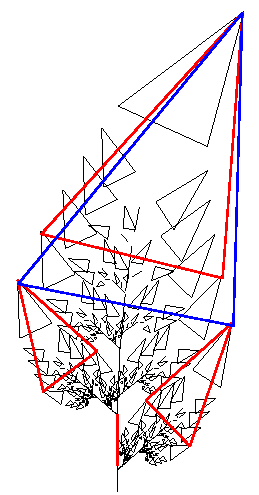
Najlepší výsledok kódovania uvedeného obdĺžnika by sme dostali, ak obrazy obdĺžnika S v afinných transformáciách by disjunktne pokryli celý pôvodný obraz. Preto je možné kolážovú teorému interpretovať nasledujúcim tvrdením: Čím presnejšie aproximuje zjednotenie transformovaných obrazov cieľový obraz, tým presnejšie je kódovanie tohto obrazu sústavou transformácií. Na nasledujúcom papradí vidieť, že časti 3 a 4 sú po transformáciách zhodné s trojuholníkom 2, kmeň papradia 1 tiež zahrnieme kvôli pokrytiu celého obrazu. Z týchto častí dokážeme s určitou presnosťou vygenerovať predchádzajúce papradie.

Komprimujeme obrázok (napríklad známa papraď). Uložené dáta budeme mať len z modrého trojuholníka (viď. obrázok nižšie) a IFS, ktorý bude popísaný troma transfomačnými rovnicami, každá z nich bude transformovať modrý trojuholník do jedného červeného. Celý obrázok vygenerujeme pomocou koláže dát pôvodného obrazu.
Ako už bolo povedané každá transformácia má tvar
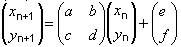
Teda z troch vrcholov pôvodného trojuholníka a troch bodov nového trojuholníka dostávame dve sústavy troch rovníc o troch neznámych.
Použitím tejto metódy je na reprezentáciu obrázka nutné ukladať dáta len istej časti pôvodného obrázku a 6 čísel, vo formáte pohyblivej rádovej čiarky, pre každú transformáciu z IFS.
Fraktálové kódovanie je stále zaujímavé najmä s ohľadom na veľké kompresné pomery. Patrí k stratovej forme obrazového kódovania, ako napríklad JPEG. Prvým, ktorý sa snažil využiť vlastnosti fraktálov a spôsob ich generovania v kompresii obrazov bol M. Barnsley. Jeho doktorand A. Jacquin ako prvý realizoval funkčnú metódu fraktálového komprimovania obrazov. Komprimácia spočíva v lokálnej samopodobnosti blokov obrazu t.j. v hľadaní nerovnako veľkých dvojíc blokov, ktoré sú štatisticky invariantné voči zmene mierky. Na tie bloky sa potom aplikujú kontraktívne transformácie.
- Krátka história:
- 1977 – Benoit Mandelbrot: Fractal geometry of Nature
- 1981 – John Hutchinson: Fractals and Self-Similarity
- 1985 – Michael Barnsley, Stephen Demko: Iterated Function Theory
- 1988 – M.Barnsley: Fractals Everywhere
- 1990-1991 – M.Barnsley: prvý a druhý patent
- 1991 – Arnaud Jacquin: prvá praktická metóda kompresie
- 1993 – M.Barnsley,L.Hurd: Fractal Image Compresion
- 1994 – vyriešenie problému rýchlosti algoritmu
- 1995 – integrácia fraktálov do waveletovej kompresie
- Momentálen sú dostupné dva kódovacie štandardy (obidva sú patentované):
- FIF (Fractal Image File)
- FFIC (Fast Fractal Image Compression)
Postup kódovania - Jacquinov kódovací algoritmus
Kódovací algoritmus využíva systém iterovaných funkcií. Ide vlastne o vylepšenú formu interpolácie.
- Pri implementácii tohto algoritmu je nutné vyriešiť tieto úlohy:
- rozdelenie obrazu na bloky
- výber metriky (rôzne druhy)
- špecifikácia diskrétnych kontraktívnych obrazových transformácií definovaných po blokoch
Prvým krokom je rozdelenie obrazu na neprekrývajúce sa bloky Ri(Range), ktoré pokrývajú celý obraz. Súčasne sa stanovia väčšie Di(Domain) bloky, ktoré sa môžu prekrývať, pričom nemusia pokryť celý obraz.
Druhým krokom je priradenie každému Ri bloku najpodobnejší väčší D blok. Aby bolo možné zistiť, ako príslušné Ri a Dj korešpondujú, je potrebné Dj blok zmenšiť na rozmer Ri bloku. Zrealizovať zmenšenie Dj bloku je jednoduché za podmienky, že rozmery Dj bloku sú mocninou dvoch-krát väčšie, ako rozmery Ri bloku. (Táto podmienka nie je z teoretického hľadiska nutná, avšak pre praktickú implementáciu býva pravidlom). Zmenšené Dj bloky môžme označiť Bj (Bj bloky sú rovnakého rozmeru ako Ri). Ak označíme túto operáciu Bj=u(Dj), pričom u je kontrakcia D bloku na R blok, potom napíšeme vzťah medzi príslušnými blokmi v tvare Ri=s*Bj+o kde parametre pre transformáciu kontrastu a jasu sa dajú jednoducho odvodiť metódou najmenších štvorcov.
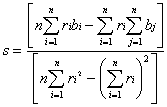
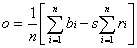
Porovnávanie Ri blokov s každým Dj má za cieľ nájsť príslušnému Ri najpodobnejší Dj blok, pre ktorý bude vzdialenosť minimálna, alebo je možné použiť iné kritérium podobnosti jednotlivých blokov.
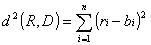
Na nasledujúcom obrázoku sú takéto sebepodobné bloky.

Komprimácia obrazu je realizovaná takým spôsobom, že sa nekóduje každý obrazový prvok, ale pre jeden Ri blok (napr. veľkosti 8x8 t.j 64 obrazových prvkov) sa kódujú v najjednoduchšom prípade parametre určujúce polohu (napr. súradnice x, y ľavého horného bodu najpodobnejšieho Dj bloku), charakteristiky bloku, t.j. hodnoty pre kontrast, jas a použitú izometriu . Výber blokov je znázornený na nasledujúcich obrázkoch.
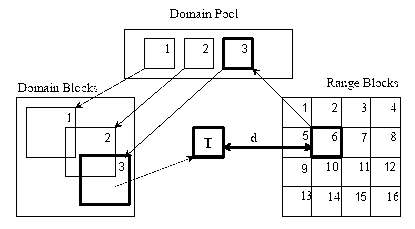
Výber blokov.
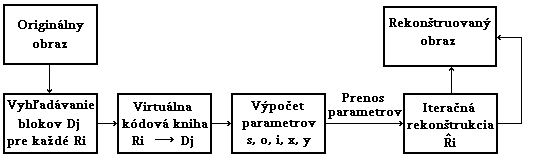
Diagram algoritmu.
Výsledky:

Pôvodný nekomprimovaný obrázok má veľkosť 184 320 bytov.
 |
 |
kvalita JPEG-max., veľkosť 32 072, |
kvalita FIF-max., veľkosť 30 368, |
 |
 |
kvalita JPEG-med., veľkosť 11 278, |
kvalita FIF-med., veľkosť 7 339, |
 |
 |
kvalita JPEG-min., veľkosť 8 247, |
kvalita FIF-min., veľkosť 3 924, |
Nevýhody algoritmu
Nevýhodou tohto algoritmu, a fraktálových kompresných algoritmov vo všeobecnosti, je jeho značná časová náročnosť na kompresiu (dekompresia je rádovo rýchlejšia). Tú zmenšujú tvz. rýchle kódovacie algoritmy , ktoré je možné principiálne rozdeliť na tie, ktoré majú alebo nemajú vplyv na kvalitu rekonštrukcie obrazu. Existujú aj ďalšie spôsoby vylepšenia algoritmov napríklad vzhľadom na zvýšenie kompresného pomeru, resp. v kombinácii s algoritmami z iných oblastí vznikajú hybridné algoritmy.
FFIC - rýchle fraktálové kódovanie.
Časovú náročnosť fraktálového algoritmu sa snaží vyriešiť zrýchlený algoritmus, ktorý je založený na rýchlom nájdení a priradení najpodobnejších D a R blokov. Výber blokov je založený na heuristických prístupoch a prehľadávaní virtuálnej kódovej knihy pomocou stromových algoritmov. Zároveň sa filtrujú a normalizujú vybrané typy blokov. V algoritme sa každý D blok zmenší na veľkosť R bloku, kvantizuje sa, robia sa na ňom úpravy ako rotácia, prevrátenie a pod. a vloží sa do stromu D blokov. Potom sa pre každý R blok vykonáva kvantizácia, úprava prehľadávacích parametrov a prehľadanie stromu, pričom D blok s najväčšou podobnosťou sa pokladá za najlepší blok z celého obrazu, to znamená, že sa neprehľadáva celý obraz, ale len niektoré časti, čo umožňuje zrýchlenie algoritmu.
Tabuľka ukazuje zrýchlenie algoritmu pri použití rozdielných parametroch β, čo je parameter vyhľadávania D blokov v strome, t.j. do akej hĺbky sa prehľadáva vytvorený strom D blokov (čím je β väčšia, tým menšia časť stromu sa prehľadáva).
| D-bloky | rms | čas(ms) | zrýchlenie | |
|---|---|---|---|---|
| úplné | 125000 | 6,7 | 8750 | 1 |
| strom (β=20) | 1954 | 7,8 | 340 | 25 |
| strom (β=100) | 306 | 8,7 | 150 | 58 |
Výsledky:
 |
 |
Originálny obraz. |
Dekódovaný obraz (úplné prehľadávanie) |
 |
 |
Dekódovaný obraz(prehľadávanie stromu, beta = 20) |
Dekódovaný obraz(prehľadávanie stromu, beta = 100) |
Naďalej sa vyvíjajú algoritmy na samotné zrýchlenie kompresie, ale aj na prepojenie algoritmov fraktálového kódovania s inými algoritmami (napr.: diskrétnej waveletovej transformácie), ktoré sa snažili odstrániť nevýhody jednotlivých prístupov a naopak využiť ich klady.
