Prírodou inšpirované algoritmy

Afinné transformácie

Kontraktor

K pochopeniu IFS z pohľadu matematiky si najprv objasníme pojem kontraktor. Kontraktor je funkcia w:X->X (X môže byť množina reálnych čísel, v priestore jedno, dvoj i viac rozmernom) s týmito vlastnosťami:

• je prostá,
• s koeficientom kontrakcie 0 <= s < 1 ,pričom platí d(w(x),w(y)) <= s * d(x,y), d je klasická Euklidovská metrika,
• po viacnásobnom aplikovaní druhej vlastnosti konverguje k fixnému bodu, ako vidieť na obrázku, na príklade jednorozmernej funkcie.

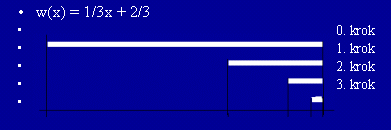
Príklad dvojrozmernej funkcie.

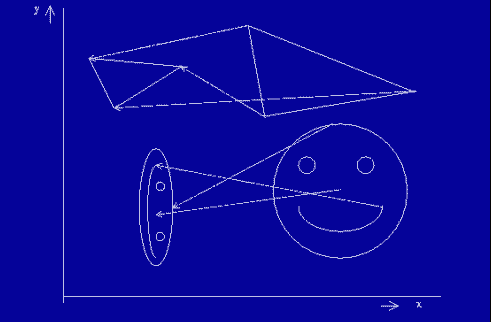
Z prvého príkladu vyplýva, že iterovaním jednej funkcie (kontraktora) dospejeme k jednému limitnému bodu, nezávisle na vstupnej neprázdnej množine. V našom prípade vstupom bola množina bodov v intervale <0; 1>, ktorá sa zmršťovala k bodu 1. V druhom príklade je uvedená jedna transformácia (iterácia) dvojrozmernej funkcie, pričom tiež je zjavné, že pôvodný obrázok sa zmenšuje.

Jeden kontraktor definovaný na dvojrozmernom priestore môžeme zapísať takto:

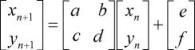
Kde a, b, c, d, e, f sú reálne čísla, xn a yn staré súradnice bodu a xn+1 a yn+1 sú nové súradnice. Je to všeobecný tvar transformačných pravidiel, ktoré opisujú afinnú transformáciu rovinného útvaru:

Atraktor je limitným prípadom uvedenej afinnej transformácie, takže jej aplikáciou na atraktor dostávame identický obrazec.

Transformačnú maticu (a, b, c, d) možno zapísať aj v tvare:

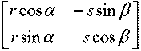
pričom r, s sú koeficienty kontrakcie v horizontálnom a vo vertikálnom smere a goniometrické funkcie uhlov α a β predstavujú pootočenie vo zvislom a vodorovnom smere pri skosení.

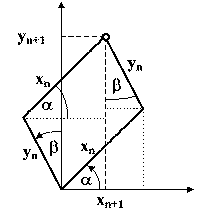
Pre hodnoty r = s = 1 sa jedná o "čisté" skosenie bez kontrakcie (predchádzajúci obrázok). Za kladný smer sa považuje pootočenie proti smeru hodinových ručičiek. Geometrický význam transformačnej matice je zrejmý zo vzťahov:

xn+1 = xn.cosα - yn.sinβ

yn+1 = xn.cosα + yn.sinβ

kde xn a yn sú dĺžky strán rovnobežníka z predchádzajúceho obrázku. Pre niektoré jednoduché transformácie nadobúda transformačná matica špeciálny tvar:

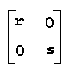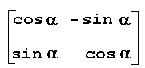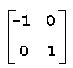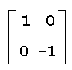α=β=0	α=β, r=s=1	α=π, β=0, r=s=1	α=0, β=π, r=s=1
kontrakcia	rotácia	preklopenie ←→	preklopenie ↑↓

Atraktor

V ďalšom použijeme na ukážku dve takéto funkcie. V každej iterácii sa vstupná množina aplikuje na obe funkcie súčasne, výsledok sa zjednotí a je vstupom do ďalšej iterácie.

Takýmto postupným generovaním dostávame množinu s nekonečným počtom bodov (množina na obrázku speje ku Cantorovej množine). Na obrázku sú tri iterácie funkcií w1 a w2 so vstupným intervalom <0; 1>. Jednotlivé obrazce v iteráciách dosiahneme aplikovaním w(K). Jednotlivé čiary tretej iterácie boli dosiahnuté takto: w1w1w1, w2w1w1, w1w2w1, w2w2w1, w1w1w2, w2w1w2, w1w2w2, w2w2w2. Výsledný obrazec sa nazýva atraktor, ktorý je tiež dosiahnuteľný z akejkoľvek neprázdnej množiny. Pozoruhodné na tom je, že konečná podoba atraktora je určená výlučne uvedenými transformáciami a nezávisí na východzom obrazci (ako to môžeme vidieť na nasledujúcom obrázku) - atraktor predstavuje podľa Banachovej vety pevný "bod" (nezávislý na počiatočnej hodnote).

Vytvorenie Sierpinského trojuholníka z odlišného východzieho obrazca.