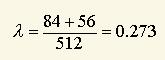Prírodou inšpirované algoritmy

Kvantitatívne hodnotenie dynamiky CA

Kvantitatívne hodnotenie dynamiky CA

Keď sa Langton zoznámil s Wolframovou klasifikáciou jednorozmerných CA, pokúsil sa detailnejšie kvantifikovať chovanie rôznych CA. Vo svojich experimentoch sa zameral na schopnosť CA prenášať informáciu. Robil to v presvedčení, že prenos a uchovávanie informácie sú základnými rysmi života. Tvrdil: Je zrejmé, že všetky živé organizmy, ktoré poznáme sú fyzikálnym stelesnením entít na spracovanie informácií. Väčšina toho čo robia nie je spracovávanie hmoty či energie, ale spracovanie informácie. Živé organizmy používajú informáciu na rozmnožovanie, na hľadanie potravy, na svoju údržbu - na zachovanie svojej vnútornej štruktúry; nakoniec štruktúra je vlastne sama o sebe informáciou.

Vo vesmíre ako celku ale panuje druhý zákon termodynamiky, podľa ktorého v uzavretom systéme entrópia rastie. Entrópia je mierou neusporiadanosti a jej rast je v zdanlivom rozpore s procesom evolúcie, vytvárajúcim naopak vysoko organizované štruktúry. Langton bol presvedčený, že existuje režim, v ktorom tento protiklad je mimoriadne výrazný.

Na hodnotenie schopnosti prenosu a uchovávania informácie systémom pravidiel CA zaviedol parameter lambda ako pomer počtu pravidiel, ktorých výstupom sú "nekľudové" stavy (keď bunka v kľudovom stave má vo svojom okolí tiež len bunky v kľudovom stave, potom sa hodnota jej stavu v ďalšej generácii nemení) k celkovému počtu pravidiel. Lambda parameter má význam len v prípade veľkého počtu sád pravidiel, kde vyhľadanie tých "najzaujímavejších" sád preskúmaním všetkých možností je nemožné. Vzťah medzi Wolframovými triedami a lambda parametrom je nasledujúci:

• malé hodnoty lambda - CA1 a CA2 (informácia je zmrazená, môže sa dlho uchovávať, ale nie je ju možné prenášať)
• veľké hodnoty lambda - CA3 (informácia sa prenáša ľahko až chaoticky, ale je obtiažne ju uchovávať)
• medzné hodnoty lambda - CA4 (prenos informácií je možný, ale nie tak rýchly, aby sa strácala väzba na jej pôvodné miesto)

Prvé dva režimy charakterizoval Langton ako nepriaznivé pre existenciu života a ten tretí ako priaznivý: život existuje na samom pokraji chaosu. Nadväzoval na názor von Neumanna, že existuje istá kritická medza zložitosti, pod ktorou sú procesy syntézy degeneratívne, ale nad ktorou má syntéza pri správnej organizácii explozívny charakter.

V prípade málo početných sád (napr. 256 sád Wolframovho 1D CA) vyššie uvedený vzťah medzi Wolframovými triedami a lambda parametrom neplatí. Hra LIFE pracuje s jednou z dvoch sád pre dva stavy a s úplným okolím, ktorých je celkom 2512 (bunka s ôsmymi susedmi umožňuje 29 = 512 pravidiel). V LIFE je nekľudovým stavom stav 1 (živá bunka), a teda v čitateli zlomku pre výpočet parametra lambda bude počet pravidiel pre zrod a prežitie. Počet pravidiel pre prežitie sa rovná

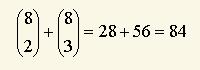
a pre zrod

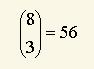
a tak