Prírodou inšpirované algoritmy

Fyzická realizácia automatu

Veľká časť tejto kapitoly je viac-menej prekladom originálu stránky CELL-AUTO.

Dnes väčšina široko-dostupného výpočtového hardwaru je stále dvojrozmerná. Väčšina procesorov v dnešnej dobe je realizovaných na jednovrstvových prípadne viacvrstvových waferoch (z anglického: wafer). Vo svojej podstate sa stále jedná iba o plochu. Akékoľvek pokusy s tretím rozmerom nezašli dosiaľ príliš ďaleko.

N-rozmerný automat v M-rozmeroch

Každá efektívna implementácia N-rozmerného celulárneho automatu by mala byť realizovaná na N rozmernom prípadne viac rozmernom substráte. To znamená, že je možné simulovať relatívne veľké jednorozmerné či dvojrozmerné automaty bez veľkej straty rýchlosti. Ak sa však pokúšame simulovať N-rozmerný automat, na menej ako N rozmernom substráte vzdialenosti medzi jednotlivými susednými bunkami v minimálne jednom rozmere narastajú s veľkosťou automatu. Chýba totiž minimálne jeden rozmer. S pridávaní nových buniek, sa tak tieto susedné bunky vzďaľujú. No čo najlepšie využitie daného substrátu je teda najvýhodnejšie ak je automat práve toľko rozmerný ako daný hardware. Použitie jednorozmerného automatu v dvojrozmernom výpočtovom systéme môže znamenať plytvanie jeho potenciálu.

Periodické štruktúry

Existuje jedna výnimka pre tvrdenie, že najvýhodnejšie je realizovať N-rozmerný automat v N-rozmernom hardware. Ak je automat periodický a teda začiatočné prvky susedia s koncovými ukazuje sa ako najvýhodnejšie použiť N+1 rozmerný priestor.

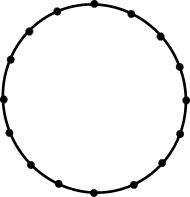
Nasledujúci obrázok vyobrazuje prípad jednorozmerného automatu. Bodky predstavujú jednotlivé bunky a čiary prepojenia, relácia susedstva.

Realizácia periodického jednorozmerného automatu v dvoch rozmeroch vyzerá nasledovne:

Nasledujúci obrázok vyobrazuje jednu možnosť realizácie takéhoto automatu v jednom rozmere.

Napriek tomu, že priestor ktorý zaberá každá buka ostal rovnaký, vzdialenosť medzi susednými bunkami sa zdvojnásobila. Ak má teda šírenie signálu veľký význam, môže sa tak stať, že sa automat virtuálne spomalí na polovičku pôvodnej rýchlosti. Iný pokus o zachovanie okupovaného priestoru bunkami môže vyzerať nasledovne:

Tento prípad má však ešte väčšiu nevýhodu. Ak by rýchlosť celého automatu závisela od najvzdialenejších buniek, potom je zrejmé, že táto implementácie povedie k výraznému spomaleniu automatu nakoľko vzdialenosť medzi prvým a posledným prvkom je niekoľkonásobne väčšia ako medzi inými susednými bunkami.

Nasledujúce diagramy slúžia na porovnanie dvoch identických dvojrozmerných automatov s jediným rozdielom a to že automat vpravo je periodický toroid zatiaľ čo automat vľavo nie je. Farebné a číselné označenie buniek zobrazuje vzťah medzi bunkami týchto dvoch automatov.

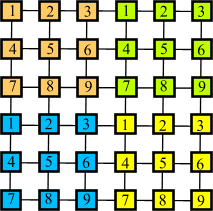
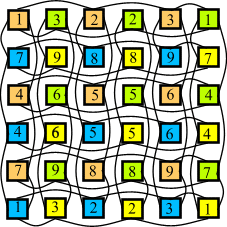
Oba diagramy vyobrazujú najefektívnejšie rozloženie buniek v dvojrozmernom priestore. Taktiež, je vhodné si uvedomiť, že samotný fakt toroidálnej štruktúry spôsobí, že sa susedné bunky od seba fyzicky vzdialia. Tým pádom je potrebné zvýšiť dĺžku prepojení a naviac jednotlivé prepojenia musia krížiť jedno druhé aby pospájali svojich susedov. Z týchto dôvodov je nutné samotné bunky oddialiť ešte viac. Ak teda rýchlosť celého automatu závisí od vzdialenosť prepojení cez ktoré sa musí signál šíriť je teda zrejmé, že takýto automat bude výrazne pomalší ako jeho neperiodická verzia. Je teda vidieť, že fyzická realizácia periodického celulárneho automatu vedie k zníženiu rýchlosti daného CA a preto je vždy výhodné pokúsiť sa vyhnúť takémuto druhu CA.