Prírodou inšpirované algoritmy

CA a L-systémy v modelovaní rastlín

Celulárne automaty

Difúzne ohraničené zhlukovanie a rast reprezentuje jeden druh rozšírenia Edenovho modelu, vysvetľujúc vznik vetviacich vzorov. Iné rozšírenie ponúka Ulam (Ulam,1962), spoluvynálezca celulárnych automatov. Celulárny automat pozostáva z buniek, usporiadaných vo zvyčajne pravoúhlej mriežke, ktoré vzájomne "komunikujú". Ulam stanovil, že nové bunky môžu byt pridané na okraj doteraz formovanej štruktúry len ak tieto bunky nekolidujú vzájomne alebo s predtým pridanými bunkami. Rozvinutie vetviacej štruktúry, nazývanej Maltézsky kríž je ilustrované v animácii. Zaujímavou vlastnosťou tohto modelu je jeho senzitivita k prostrediu. Napríklad animácia ukazuje rozvíjanie maltézskeho kríža spojené s prekážkou (biela farba). Aj keď sa štruktúra trochu zmenila, prispôsobila sa prítomnosti prekážky a narastala okolo bez zachytenia vetvení. Trojrozmerné rozšírenie tejto základnej koncepcie bolo aplikované Greenom (Green,1991) pri modelovaní rozvíjania sa koreňov stromu okolo kameňov v zemi ako je to na obrázku dole. Podobný spôsob bol použitý v (Green,1989) na simuláciu rastu vínnej révy okolo domu.

L-systémy

Modely rastlín ktoré boli popísané v predchádzajúcom majú dve obmedzenia. Prvým je, že sú neobyčajne oportunistické: narastanie štruktúry je riadené takmer výlučne okolitým prostredím. V skutočnosti veľkosť rastlinných štruktúr je daná genetickými faktormi. Naviac všetky modely, ktoré boli popísané doposiaľ predstavujú narastajúci vývin: to znamená, že proces vývinu štruktúry je daný postupným pridávaním nového materiálu.

Avšak vývojové štruktúry vyšších organizmov sú často oveľa komplikovanejšie. Napríklad v priebehu vývoja stonky s listami, animácii, vrchol stonky vytvára sled listov, ktorých veľkosť rastie a zároveň narastá dĺžka stonky a uhol jednotlivých odbočení. Zmeny uhla jednotlivých odbočení a dĺžka stonky sú nerastúcou súčasťou tohto procesu. Podobné javy môžeme pozorovať vo vývine výhonkov Fraximus pennsylvanica (jaseň cervený). Animácia ilustruje tento vývin z fixného bodu pohľadu, kým animácia ukazuje tú istú simuláciu z pohľadu kamery zaostrenej na vrchol výhonku. Zaznamenávame postupné predĺženie stonky a zmeny v uhle jednotlivých vetiev. V animácii vidno tiež pohľad na výstup výhonku z púčiku. Na zachytenie takýchto nerastúcich, vnútorne budených procesov, Lindenmayer (Lindenmayer,1968) navrhol model rozvíjania na základe prepísateľných symbolov a pravidiel,ktorý môžeme považovať za špeciálny prípad celulárnych automatov.

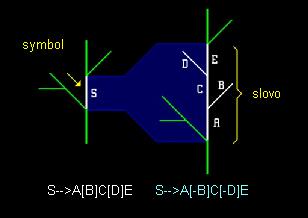
Pravidlá L-systému

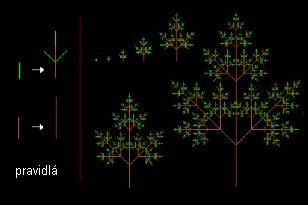
Tento model, známy ako L-systém, pôvodne poskytujúci formálny popis vývoja jednoduchého viacbunkového organizmu, ktorý bol neskôr rozšírený na vyššie rastliny. Prepísateľné pravidlá obsluhujú všetky moduly rastliny: ako sú vrchol, stonka alebo listy. Každé pravidlo pozostáva z dvoch častí : symbol a slovo, ako je znázornené na obrázku. Počas odvodenia nasledujúceho kroku je symbol nahradený slovom. Lindenmayer používa zápis pomocou reťazcov, pretože je jednoduché rozpísanie pravidiel a vykonanie simulácie. Veľmi jednoduché L-systémy môžu vytvoriť rastlinám podobné štruktúry. Napríklad obrázok ukazuje L-systém s dvoma pravidlami. Prvé pravidlo určuje, že vetva vytvára vetviacu štruktúru s troma vetvami a stonkou. Druhé pravidlo predlžuje dĺžku stonky. Pravidlá sú invariantné vzhľadom k mierke, to znamená, že ak zmeníme veľkosť prvej časti pravidla nejakým faktorom r, mali by sme preškálovať druhú časť pravidla tým istým faktorom.