Prírodou inšpirované algoritmy

Modely jednoduchých štruktúr

Edenov model

Použitie reakčno-difúzneho modelu je obmedzené jednou podmienkou, ktorú vyslovil Turing : prostredie v ktorom sa reakčná difúzia uskutočňuje, plocha alebo krivka, nenarastá (nevyvíja sa). Jeden z prvých počítačových modelov vývoja biologických štruktúr bol navrhnutý Edenom (Eden,1960). Edenov model je veľmi jednoduchý. Simulácia sa uskutočňuje v pravouhlej mriežke. Jednoduchá elementárna častica je umiestnená v strede tejto mriežky. Nasledujúce častice sú postupne pripojené k náhodne vybraným bodom na okraji štruktúry formovanej v predchádzajúcich krokoch. Príklad štruktúry získanej týmto spôsobom je ukázaný na obrázku. Farby indikujú stav štruktúry v odlišnom čase. Štruktúra rozvinutá podľa Edenovho modelu je približne kružnicového tvaru.

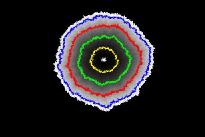
Edenov model

Difúzne ohraničené zhlukovanie

V roku 1983 Witten a Sander (Witen & Sander,1983) modifikovali Edenov model za predpokladu, že čiastočky vznikajú veľmi ďaleko od rozvíjajúcej sa štruktúry a uskutočňujú náhodnú cestu v okolitom priestore. Ak čiastočka narazí do štruktúry, prilepí sa k nej. Tento model bol nazvaný difúzne ohraničené zhlukovanie (DLA - diffusion limited aggregation ), pretože náhodné pohyby čiastočiek môžu byť zobrazené ako difúzia na molekulárnej úrovni. Hoci rozdiel medzi činnosťou Edenovho modelu a difúzne ohraničeného zhlukovania sa zdá pomerne malý, rozdiel vo výslednom vzore je výrazný.

Difúzne ohraničené zhlukovanie

V protiklade s Edenovým približne kruhovým obrazcom, DLA model produkuje fraktálnu vetviacu štruktúru ako vidno na obrázku. Mandelbrot a Evertsz (Mandelbrot & Evertsz,1990) ponúkajú vizuálne vysvetlenie tohto tvaru v animácii. Oni vykresľujú priemernú koncentráciu čiastočiek v priestore okolo rastúcej štruktúry prostredníctvom riešenia Laplaceových rovníc v tomto priestore. Okrajové podmienky predpisujú vysoké koncentrácie čiastočiek na vonkajšom okraji priestoru a nulové na hranici fraktálu. Zelená farba v pozadí indikuje vysokú koncentráciu čiastočiek v priestore a čierna indikuje nízku koncentráciu. Niektoré línie konštantnej koncentrácie boli zvýraznené na uľahčenie interpretácie obrázku. Je jasné, že koncentrácia čiastočiek medzi vetvami je vždy veľmi nízka, čo je dôvod prečo v týchto miestach vetvy nenarastajú. Na druhej strane vrcholky štruktúry sú veľmi blízko oblastí s vysokou koncentráciou čiastočiek, čo je dôvod ich rýchlejšieho rastu. Obrázok ukazuje difúzne ohraničené zhlukovanie, kde počiatočná štruktúra je horizontálna čiara.

Pohybujúce sa čiastočky môžu predstavovať zložky výživy, využívané jednoduchou rastúcou štruktúrou (napr. kolónia baktérií) na jej vlastné formovanie. Rozdiel medzi difúzne ohraničeným zhlukovaním (kde sú čiastočky jednoducho prilepené k rastúcej štruktúre) a difúzne ohraničeným rastom (kde čiastočky sú transformované na telo organizmu) bol prvýkrát popísaný Meakinom (Meakin,1986). V tomto význame Edenov model popisuje rast bakteriálnej kolónie pri dostatku živín. Štruktúra sa rozvíja všade kde je priestor na expanziu. Difúzne-ohraničený rast sa vyskytuje tam, kde sú živiny vzácne. Štruktúra využíva všetky živiny vo svojom okolí a narastá v smere príchodzích živín. Matsushita a Fujikawa (Matsushita & Fujikawa,1990;Fujikawa & Matsushita,1991) experimentálne ukázali, že v závislosti na dostupnosti živín kolónie baktérií majú tiež približne kruhovú alebo vetviacu štruktúru.

Difúzne ohraničený rast húb.

Jeden z difúzne ohraničených rastúcich modelov bol navrhnutý Kaandorpom (Kaandorp,1992;Kaandorp,1994), ktorý simuluje rast morských prísavných organizmov, najmä koraly a hubky. Veľkosť výrastku je určená lokálne prostredníctvom dostupnosti živín, rozptýlených vo vode v okolí organizmu. V blízkosti k oblastiam organizmu, ktoré majú vysoké zakrivenie, gradient koncentrácie živín je vysoký, a štruktúra prudko rastie. Blízko plochých oblastí, kde gradient koncentrácie je nízky štruktúra sa rozvíja pomalšie. Simulácia vývoja morskej hubky použitím tejto techniky je ukázaná v animácii.