Prírodou inšpirované algoritmy

Vznik samoreprodukcie

Táto kapitola je prakticky prekladom druhej časti článku Reggia, Chou, Lohn, 1998

Doteraz popísané samoreprodukujúce sa štruktúry boli na začiatku nastavené ako pôvodné kópie štruktúry, ktoré sa budú reprodukovať ("semeno" - počiatočné štruktúry) a sú založené na ručne vytvorených pravidlách zmien určených pre jedinú konkrétnu štruktúru. Nedávno sme sa začali uberať iným smerom pri vytváraní samoreprodukujúcich sa štruktúr, pričom sme sa na samoreprodukciu zamerali ako na vznikajúcu vlastnosť (emergent property). V tejto časti ukážeme dva príklady našej práce v tejto oblasti.

Vznik replikátorov

Naše nedávne práce ukázali, že je možné vytvoriť modely celulárnych automatov, v ktorých samoreprodukujúce sa slučky vznikajú z počiatočného stavu s náhodnou hustotou a rozložením prvkov (tzv. "počiatočná polievka" - "primordial soup") (Chou & Reggia, 1997). Tieto vzniknuté samoreprodukujúce sa slučky používajú množinu všeobecných pravidiel, ktoré podporujú reprodukciu a rast slučiek rôznych veľkostí. Táto množina pravidiel tiež umožňuje náhodné zmeny veľkostí slučiek a vzájomné pôsobenie samoreprodukujúcich sa slučiek v priestore celulárnych automatov, obsahujúcich voľne pohyblivé prvky. Príklad bežiaci v malom priestore (40x40) celulárnych automatov s náhodným východzím stavom s hustotou prvkov 25% je na nasledujúcom obrázku. Keďže sú použité okrajové pravidlá na to, aby sa náprotivné okraje brali ako spojené, priestor je v skutočnosti guľový. Na začiatku, v čase t=0, je 25% priestoru vyplnených náhodne umiestnenými, nerozmnožujúcimi sa prvkami, označenými znakmi O, > alebo L, zatiaľ čo bunky v pokojovom stave sú znázornené ako prázdne miesta. Všetky prvky, okrem >, o ktorom hovoríme, že je orientovaný, majú silnú rotačnú symetriu.

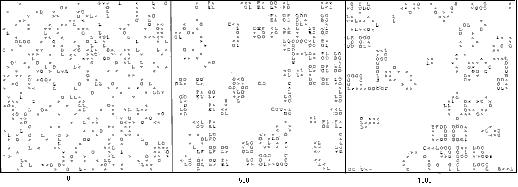
Táto simulácia sa vyznačuje počiatočným vznikom veľmi malých samoreprodukujúcich sa slučiek a ich postupným vývinom až na stále väčšie a rôzne reprodukcie. Počas tohto procesu sa môže reprodukujúca slučka stretnúť s inými slučkami alebo s voľne sa pohybujúcimi prvkami a buď sa vráti do pôvodného stavu, alebo sa zničí. Po čase t=500 sa objavujú veľmi malé samoreprodukujúce sa slučky o veľkosti 2x2 a 3x3. Po čase t=1500 sa práve slučka o veľkosti 4x4 chystá vytvoriť slučku 5x5 v strede ľavej časti. V čase 3000 je najväčšia slučka veľkosti 8x8 a je v stave pred vytvorením slučky 9x9. Po čase 5000 veľa veľmi veľkých slučiek sa navzájom ničí a ostáva len jedna nedotknutá slučka o veľkosti 10x10. Po čase 7500 "vymierajú" všetky veľké slučky, ale objavujú sa nové slučky 3x3. Tieto sa budú reprodukovať, pričom nie je jasné kedy (ak vôbec niekedy) sa samoreprodukcia zastaví. V tomto príklade sa rozmery reprodukujúcich sa štruktúr stali príliš veľkými aby sa pohodlne prispôsobili takému malému priestoru (len 40x40) a veľké slučky prejavovali sklon k vzájomnému ničeniu.

Ako sa dá z tohto príkladu vidieť, funkcia zmien týchto samoreprodukujúcich sa slučiek sa líši od tých, ktoré boli použité v predchádzajúcich modeloch celulárnych automatov v niekoľkých bodoch. Samoreprodukujúca štruktúra vzniká z náhodného počiatočného usporiadania prvkov, samoreprodukcia nie je daná na začiatku, ale vzniká v prostredí voľne sa pohybujúcich prvkov, potomkovia rastú a s časom menia svoju veľkosť a keď reprodukcia už nie je možná, podliehajú zničeniu. Všetko toto sa objavuje v prítomnosti jedinej prechodovej funkcie založenej na 9 bunkovom okolí. Tak ako je stále viac používaná v modelovaní celulárnych automatov, prechodová funkcia je založená na funkčnom delení údajových polí (Toffoli & Margolus, 1987). Ako vidíme na ďalšom obrázku, bitová hĺbka bunky celulárneho automatu (v našom prípade 8 bitov) sa funkčne rozdelí na 4 rôzne polia (po 4, 2, 1 a 1 bite) tak, že každé pole obsahuje iné významy a funkcie na ovládanie zapisovača. Využitie delenia polí veľmi zjednoduší programovanie pravidiel celulárnych automatov a výsledné pravidlá sú pomocou neho oveľa čitateľnejšie. Na ilustrácii v tomto článku je zobrazené len pole prvkov.

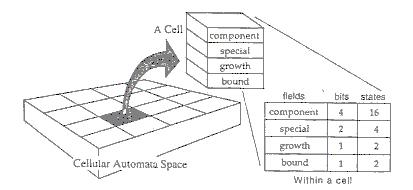
Ako bolo skôr poznamenané, každá bunka, ktorá nie je v pokoji predstavuje možný "prvok" štruktúry celulárnych automatov. Štruktúrou celulárnych automatov môže byť aj jediná bunka, t.j. bunka bez žiadneho významového prepojenia s nejakou vedľajšou činnou bunkou, a v tom prípade ju voláme neviazaným prvkom. Na druhej strane, štruktúra celulárnych automatov sa môže skladať z niekoľkých susediacich činných buniek ktoré sú navzájom funkčne pospájané, správajú sa ako celok, tak ako samoreprodukujúca sa slučka. V tomto druhom prípade voláme túto štruktúru štruktúrou s viacej prvkami, alebo jednoducho štruktúrou a jej prvky voláme viazanými prvkami. (ich bit viazania je nastavený na 1; pozri predchádzajúci obrázok).

Spomínané štyri údajové polia (predchádzajúci obrázok) a ich poradie vo funkcii zmien je nasledovné. Štvorbitové pole prvok obsahuje jednu z 12 hodnôt stavov (z možných 16) prislúchajúcu nejakému prvku tak, ako sme videli v predchádzajúcich príkladoch. Sem patria: O (tvorí signálovú cestu), > (signál rastu signálovej cesty, predstavuje vlastne 4 stavy), B (narodenie novej prvky - Birth), L (signál zatočenia doľava - Left), C (roh - Corner) a D, E, F (vetvenie/oddelenie). Je tu tiež ešte pokojový stav, ktorý je všade zobrazený ako prázdne miesto. Ostatné polia sú nové. Dvojbitové pole zaznamenáva výnimočné situácie, ktoré vznikajú zriedkavo v priestore celulárnych automatov. Sú to napríklad vetvenie, blokujúci signál na údajovej dráhe alebo zánik slučky. Jednobitové pole rast v stave 1 označuje podnet, ktorý môže spôsobiť, že súčasná postupnosť signálu zväčší svoju dĺžku. Jednobitové pole viazanie v stave 1 označuje bunku ako časť viacbunkovej štruktúry; ináč je táto bunka neviazanou zložkou.

Úplná množina pravidiel tvoriacich prechodovú funkciu podporuje reprodukciu slučiek podobným spôsobom ako v minulosti (Langton, 1984; Lohn & Reggia, 1995). Navyše však môže byť potomok inej veľkosti (väčší) a tento proces nazývame rozšírenou reprodukciou. Postupnosť signálov slučky sa dá zmeniť tak, aby vytvárala slučky väčšie ako je sama ak sa v niektorej bunke slučky náhodou objaví bit rastu v stave 1 (činné) počas vetvenia ramena. Pravidlá celulárnych automatov, ktoré podporujú rozšírenú reprodukciu sú nové. V minulosti bolo treba pre každú veľkosť bunky inú množinu pravidiel; tu je vznik slučiek s inou veľkosťou a ich súčasná reprodukcia podporovaná jedinou množinou pravidiel. Toto umožňuje počiatočnej malej vznikajúcej samoreprodukujúcej sa štruktúre rásť.

Ďalšou novou stránkou tohoto modelu je zisťovanie stretávania (zrážania) sa a rozkladania sa. Vo všetkých minulých prácach o samoreprodukujúcich sa slučkách sa reprodukcia objavuje v prázdnom priestore a funkcia zmien nemusí narábať s neočakávanými udalosťami. Inými slovami, zatiaľ čo zapisujete pravidlá, máte úplnú kontrolu nad správaním, ktoré sa objavuje v priestore celulárneho automatu, vrátane počiatočného stavu. Naproti tomu, prvý predpoklad je, že nejestvujú predbežné znalosti o vzájomnom pôsobení medzi slučkami, alebo o tom ako vyzerá priestor celulárneho automatu v čase nula. Hoci pravidlá, s ktorými sme doteraz uvažovali v predchádzajúcich modeloch reprodukcie, dokážu spoľahlivo viesť štruktúru k samoreprodukcii v izolácii, nedokážu zaručiť, že štruktúra nevojde do inej štruktúry, že sa nebudú pokúšať reprodukovať dve štruktúry naraz do tej istej oblasti priestoru, alebo že slučka sa nestretne s voľne pohyblivým neviazaným prvkom. Všetky tieto činitele sú určované náhodne. Tu použitá prechodová funkcia teda predpokladá, že nie všetky vytvorené bežné činnosti pôjdu vždy za sebou bez prerušenia alebo rušenia od ostatných štruktúr. Zahŕňa v sebe pravidlá, ktoré budú zisťovať činnosti, ktoré zlyhali a čistiť priestor celulárneho automatu po takomto zlyhaní. Keď hocijaká z buniek slučky sa dostane do stavu zlyhania, tento stav sa rýchlo šíri po celej štruktúre, čo spôsobí, že sa slučka úplne rozpadne. Prvky slučky sa stanú neviazanými a znova sa začnú riadiť pravidlami pre neviazané prvky.

Nejestvuje žiadna predbežná informácia o tom, kedy a kde by mal byť v modeli vznikajúcej reprodukcie nastavený bit rastu a žiadny z nich nie je nastavený na začiatku. V príklade, ktorý sme uviedli, vždy keď sa rozpadne alebo "umrie" signál L, na svojom mieste zanechá bit rastu. Slučka má obyčajne len jeden L signál, takže jedna rozpadajúca sa slučka obyčajne spôsobí vytvorenie jedného nového bitu rastu v priestore celulárneho automatu. Bit rastu sa použije počas fázy vetvenia slučky na rameno za účelom rozšírenia postupnosti signálov v slučke. Ako ukazuje nasledujúci obrázok, toto sa deje v dvoch krokoch. Najprv ak signál > nájde na svojom mieste bit rastu a je to posledný signál > pred signálom L, neskopíruje za sebou signál L ako to robí obyčajne. Namiesto toho ešte raz ostane na svojej súčasnej hodnote >, čiže vlastne rozširuje postupnosť signálu o jeden prvok. Signál L na chvíľu zmizne pretože nebol skopírovaný, ale znovu sa objaví, keď signál > uvidí signál F na ktorého mieste je bit rastu. Akonáhle znova získame signál L, bit rastu sa nastaví na 0, takže už nespôsobí ďalší podnet na rast. Takže keď slučka zomrie, zanechá za sebou bit rastu a keď sa zväčšuje, spotrebuje bit rastu. Toto poskytuje zaujímavý ekologický činiteľ kolísania vo vesmíre celulárnych automatov.

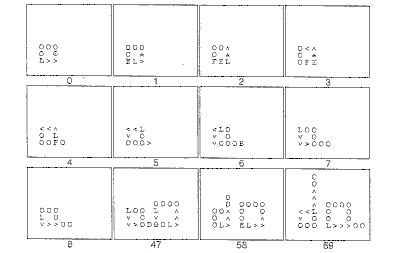
Vznik samoreprodukcie sa dosiahol povolením premiestňovania a premieňania neviazaných prvkov a ich nahodným objavovaním, t.j. "miešaním počiatočnej polievky", až kým sa náhodou neobjaví usporiadanie prislúchajúce malej (2x2) slučke. Pravidlá, podľa ktorých sa toto deje sa dajú zhrnúť ako:

• Ak má nečinná bunka práve troch susedov, stane sa činnou v ďalšom kroku. Jej činná hodnota je určená stavmi jej susedov
• Ak má činná bunka práve dvoch alebo troch činných susedov, ostane činnou, ináč sa činná bunka v ďalšom časovom kroku vráti do pokojového stavu

Tieto pravidlá sú zovšeobecnením (z binárnych do nebinárnych stavov) tých, ktoré boli použité v hre života a vo všeobecnosti vytvárajú neustále sa meniace rozloženie neviazaných prvkov. Všetko, čo je potom potrebné ku vzniku samoreprodukcie je malá množina pravidiel, ktoré sledujú informácie o usporiadaní najmenšej slučky. Keď sa takéto usporiadanie objaví, všetky štyri jej členy naraz zmenia svoj bit viazania (bound bit) na 1 a v ďalšom časovom kroku tak vytvoria činnú najmenšiu slučku. Takto vzniká prvý samo sa reprodukujúci prvok. Toto je možné len s použitím miestnych (lokálnych) činností), pretože minimálne usporiadanie slučky je tak malé, že sa prispôsobí aj v 9 bunkovom okolí, pričom každý prvok "vidí" to isté usporiadanie. Príklad ako pracuje množina pravidiel neviazaných prvkov a ako vedie k prvej samo sa reprodukujúcej štruktúre je predvedený na nasledujúcom obrázku.

Správanie tohto modelu vznikajúcej samoreprodukcie bolo preverené experimentálne (Chou & Reggia, 1997). Bolo prevedených 81 simulácií, pričom sa menila veľkosť priestoru celulárneho automatu (50x50, 100x100, 150x150, 200x200), počiatočná hustota neviazaných prvkov (10%, 20%, 30%, 40%, 50%) a náhodné počiatočné usporiadanie pri každej simulácii. V 80 z týchto 81 simulácií vznikla samoreprodukcia a obyčajne v nich prežívala natrvalo. Zistilo sa, že vznik, množenie a životnosť samoreprodukujúcich sa slučiek je silným javom, pomerne necitlivým ku počiatočným podmienkam simulácie. Existuje veľmi stála a charakteristická dynamika tvoriaca základ množiny pravidiel vznikajúcej samoreprodukcie. V skutočnosti počet činných buniek a podiel viazaných/neviazaných prvkov, sa vždy približoval k dlhodobo stálej hodnote. Táto hodnota závisí na vzájomnom pôsobení medzi pravidlami ovládajúcimi reprodukciu a pravidlami ovládajúcimi pohyb neviazaných prvkov a nie len na niektorej podmnonožine týchto pravidiel. Vo všeobecnosti počet a veľkosť reprodukujúcich sa slučiek sa tiež ustáli. Po niekoľkých tisícoch časových krokov zvyčajne nenastáva žiadna výrazná zmena v priemernom počte a priemernej veľkosti slučiek v priestore celulárneho automatu. Tieto hodnoty vykazovali nepravidelnosť a kolísanie s meniacou sa výchylkou okolo priemernej hodnoty, poukazujúc na dynamiku chaosu.

Tieto výsledky po prvý raz ukazujú, že neobyčajné samoreprodukujúce sa štruktúry môžu vzniknúť v priestore celulárneho automatu spusteného s náhodne rozloženou množinou prvkov. Bolo vykonaných aj niekoľko ďalších výpočtových výskumov vznikajúcej samoreprodukcie (pozri kapitolu 28 v Koza, 1992) a (Pargellis, 1992), ale tieto nepoužívajú metódy celulárnych automatov. Napríklad výskum v (Pargellis, 1992) používal veľmi rozličné modely (necelulárne automaty), ktoré mali počiatočný stav zložený z náhodne vytváraných postupností počítačových operácií. Tento model vyvinul samoreprodukciu pomocou operácie premeny (mutation operation). Prvotný záver urobený z výsledkov bol taký, že pravdepodobnosť zmeny náhodne vytvorenej postupnosti operácií na samoreprodukujúcu slučku sa zvýšila s počtom operácií, ktoré obsahovala. Navyše samoreprodukujúce sa postupnosti sa zmenšovali len čo sa objavili. Tu popísaný model celulárneho automatu ukazuje, že také správanie nie je nutne prirodzenou stránkou vznikajúcej samoreprodukcie a že najprv môžu vzniknúť malé reprodukujúce sa štruktúry a tie potom môžu narásť na väčšie, ako sa často dohadujeme, že to nastalo pri počiatku biologickej reprodukcie. Rozdiely vo výsledkoch pripisujeme skutočnosti, že náš model začína s náhodnými jednotlivými zložkami a nie náhodnými počiatočnými postupnosťami počítačových operácií, že ich pravidlá boli umelo vytvorené a že celulárne automaty sú založené výlučne na vysoko miestnych operáciách (napríklad nejestvuje žiadna celková operácia kopírovania, ktorá kopíruje slučku do susednej oblasti priestoru).

Vyvíjajúce sa reprodukčné pravidlá

Predchádzajúce výpočtové modely samoreprodukcie používajúce celulárne automaty boli navrhnuté ručne, čo je zložitý a časovo náročný proces, ktorý programátor vynaloží na úkor svojich vedľajších záujmov. Druhou možnosťou, na ktorú sme nedávno ukázali je možnosť vynájsť pravidlá pre samoreprodukciu samočinne použitím genetických algoritmov (Lohn & Reggia, 1995, 1997). Zatiaľ čo práce v tejto oblasti sa len začínajú a štruktúry doteraz použité sú celkom malé, prvé výsledky už vytvorili novú triedu reprodukujúcich sa štruktúr, ktoré sa už nerozmnožujú tak ako predchádzajúce, ale novým nezvyčajným spôsobom.

Pomerne málo predchádzajúcich štúdií sa zmieňovalo o používaní genetických algoritmov (alebo podobných postupov) na samočinné vytváranie tabuliek pravidiel pre celulárne automaty (pozri napríklad Andre et al., 1997; Mitchell & Hraber, 1993). S výnimkou predbežnej správy (Lohn & Reggia, 1995), neexistujú žiadne predchádzajúce správy o použití genetických algoritmov na objavovanie samoreprodukujúcich sa štruktúr v modeloch celulárneho priestoru. Takýto výskum sa s najväčšou pravdepodobnosťou neuskutočnil z najmenej dvoch príčin. Po prvé, výpočtová zložitosť sa môže stať neúnosnou. Tabuľky pravidiel pre malú sústavu môžu rýchlo rásť do extrémnych rozmerov (napr. 25000 pravidiel zmien pre 10 stavové, 5 bunkové okolie, model so silnou rotačnou symetriou), a práca s početnou tabuľkou pravidiel pomocou genetických algoritmov je výpočtovo veľmi drahá. Po druhé, zistenie účinnej funkcie schopnosti je zložitá úloha. Očividne zrejmé funkcie schopnosti, ako napr. tie, ktoré len počítajú počet replikantov, sú bezvýznamné na začiatku, keď ešte žiadne replikanty nie sú. Taktiež porovnávanie vyvíjajúcej sa štruktúry s predurčeným replikantom pomocou súhlasných vzoriek nedáva čiastočný úžitok počas samotného reprodukčného cyklu, keď štruktúra mení svoje usporiadanie zatiaľ čo sa reprodukuje. Ďalej nie je dopredu zrejmé, v ktorých časových krokoch sa rozhodne o vlastnostiach reprodukcie. Použitie údajov celulárneho priestoru z jediného časového kroku by vyžadovalo dopredu vedieť v akom usporiadaní sa replikanty objavia a predpokladá, že replikanty sa objavujú všetky naraz a nie v rôznych krokoch.

Našťastie dokázalo sa, že je možné vyriešiť tieto problémy aspoň do istej miery (Lohn & Reggia, 1995, 1997). Genetický algoritmus, ktorý sme použili začína vytváraním skupiny náhodne inicializovaných tabuliek pravidiel a tieto používa na spustenie simulácií celulárnych automatov, pričom všetky začínajú s tou istou počiatočnou štruktúrou. Následkom týchto simulácií každá tabuľka pravidiel v skupine prijíma mieru schopnosti F, ktorá odráža stupeň v akom sa v nej objavujú prechodové pravidlá sľubujúce podporu samoreprodukcie. Potom sa vytvorí nová skupina, pričom sa náhodne vyberajú tabuľky pravidiel tak, aby ďalej pokračovali vo vytváraní novej skupiny primerane k ich schopnosti. Keď sa vytvorí nová skupina, tabuľky zo starej skupiny sa kombinujú krížením a náhodne sa mutujú. Bežne použité hodnoty parametrov v sebe zahŕňajú skupinu 100 tabuliek pravidiel a vyše 2000 generácií s pravdepodobnosťami kríženia a mutácie 0,8 a 0,1. Na konci tohoto procesu sa vráti najvodnejšia tabuľka ako potenciálna prechodová funkcia podporujúca samoreprodukciu v danej počiatočnej štruktúre.

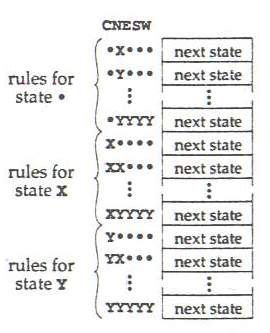
Ďalší obrázok ukazuje kódovanie tabuľky pravidiel používanej genetickým algoritmom v tomto procese. Tabuľka je indexovaná naľavo vzorkami pätbunkového okolia CNESW (center, north, east, south, west) a pravidlá pre každú jednotlivú zložku sú zoskupené spolu. Každé pravidlo má položku "nasledujúci stav", ktorá udáva, čím by sa v nasledujúcom časovom kroku mala stať prostredný bunkový prvok C pre danú vzorku oblasti. Prijatím dohody, že pravidlo pre každú možnú vzorku oblasti musí byť uvedené v tabuľke pravidiel a že tieto sú vždy v rovnakom usporiadaní, nie je výlučne potrebné ukladať vzorky okolia CNESW. "Chromozóm" (tabuľka pravidiel) je teda reprezentovaná len ako zoznam položiek nasledujúcich stavov. (t.j. len zoznam nasledujúcich stavov zaznačených na pravej strane na nasledujúcom obrázku). Pre simulácie opísané nižšie sa "chromozómy" skladali zhruba z 850 prvkov nasledujúcich stavov.

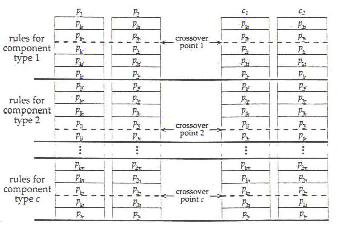
Použitá bola verzia viacbodového kríženia, kde sa aplikuje jednobodové kríženie na segmentoch (označených hrubými čiarami v ďalšom obrázku; súčasné typy prvkov majú oveľa viac pravidiel zmien ako je zobrazených tu). Bod kríženia bol vybraný náhodne pre každý segment a jednobodové kríženie sa previedlo na každom segmente. Zmyslové výsledky porovnávajúce túto metódu kríženia k jednobodovému kríženiu (po celej tabuľke pravidiel) ukázali lepší výkon pre opakované použitie krížení. Po selekcii a krížení bolo každé pravidlo zmeny podrobené mutácii, ktorá nastala náhodnou selekciou nového stavu s malou pravdepodobnosťou.

Vytváranie funkcie schopnosti F, ktorá presne meria schopnosť tabuľky pravidiel vytvoriť samoreprodukciu ľubovolnej počiatočnej štruktúry bola najnáročnejšia stránka tejto práce. Žiadna z počiatočných náhodných tabuliek pravidiel nevytvára replikanty, takže v tomto zmysle má každá nulovú schopnosť (pri rozsahu od 0 do 1). Tento problém bol odstránený vytvorením funkcie schopnosti F, ktorá je váženým súčtom troch veličín, F = wgfg + wpfp + wrfr, kde w sú pevné váhy (0 < w < 1) a f sú stupne schopnosti (0 <= f <= 1). Hlavnou myšlienkou je, že prechodné stavy na ceste k vzniku pravidiel pre samoreprodukciu je vlastne vývoj množiny pravidiel, ktoré vytvárajú rast a/alebo usporiadania podobné tým, aké sa nachádzajú v počiatočnej štruktúre. Celková schopnosť F obsahuje stupeň rastu fg, ktorý odhaduje rozsah, do ktorého prvok každého typu v danej počiatočnej štruktúre vytvára jeho stúpajúcu zásobu z jedného časového kroku do druhého a pomerné meradlo polohy fp odhadujúce rozsah, do ktorého každý prvok má po čase tie isté susedné prvky ako v počiatočnej štruktúre. Vysoké hodnoty fg a fp neznamenajú nevyhnutne, že je reprodukcia prítomná (hoci ak prítomná je, tieto čísla by mali byť vysoké), ale predstavujú situácie, ktoré by mohli byť predchodcami reprodukcie. Tretí výraz v F, stupeň replikantu fr, je funkciou súčasného počtu prítomných replikantov. Kým fr má hodnotu nula pre veľa prvých generácií s tabuľkou pravidiel, môže spôsobiť veľký rast v F, ak sa objaví reprodukcia.

Akým spôsobom by mali byť tieto tri výrazy volené, aby maximalizovali pravdepodobnosť úspechu týmto postupom? V súčasnosti nie je na túto otázku žiadna presná odpoveď. Opakované pokusy naznačujú, že wg = 0,05, wp = 0,75, wr = 0,2 je primerane dobrá množina hodnôt, keď súčet váh je ohraničený hodnotou 1 (Lohn & Reggia, 1997). Inými slovami, ukazuje sa, že pomerné meradlo polohy fp je rozhodujúcim činiteľom v objavovaní pravidiel pre samoreprodukciu.

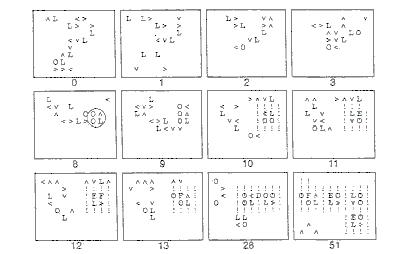
Aby sme odhadli úspešnosť predchádzajúceho prístupu, urobili sme 100 pokusov s každým z niekoľkých malých ľubovoľných počiatočných usporiadaní. Stupeň úspešnosti v objavovaní pravidiel vedúcich k vytváraniu samoreprodukcie sa prudko znižoval keď sa zvyšoval počet prvkov v počiatočnej štruktúre. Pri najlepších podmienkach bolo percento spustení, v ktorých genetický algoritmus objavil tabuľku pravidiel, ktorej výsledkom bola samoreprodukcia 93% pre štruktúry s dvomi prvkami, 22% pre štruktúry s tromi prvkami a 2% pre štruktúry so štyrmi prvkami. Ukážkový príklad samoreprodukujúcej sa štruktúry objavenej týmto spôsobom je na nasledujúcom obrázku. Tento samoreprodukujúci sa útvar je typickým príkladom. Je to štvorzložkový replikátor pre ktorý sa dajú získať mnohé replikanty za t = 5. Ako aj samoreprodukujúce sa slučky, aj tieto štruktúry postupne utvárajú rozširujúce sa kolónie.

Na replikátory objavené týmto spôsobom (genetickým algoritmom) sa môžeme pozerať tak, že tvoria tretiu triedu samoreprodukujúcich sa štruktúr (prvé dve sú univerzálne počítače - konštruktéry a samoreprodukujúce sa slučky). Okrem toho, že sa vytvárajú z ľubovolných neslučkovitých počiatočných usporiadaní, navyše sa všeobecne pohybujú po bunkovom priestore, pričom ako sa hýbu, robia kópie, čo je konštrukcia, ktorá nebola doteraz v ručne vytvorených reprodukčných modeloch celulárnych automatov zrejme ešte nikdy prijatá. Napríklad na štvorprvkový replikátor na predchádzajúcom obrázku sa môžeme pozerať akoby prechádzal premenami pri posuvnom pohybe doprava (vzhľadom na jeho počiatočnú polohu, ktorá je označená počiatkom ľubovoľných súradnicových osí v obrázku), opakovane sa objavuje vo svojom pôvodnom tvare (t = 3, 6, ...) kým odovzdáva replikanty v hornom pravom kvadrante (t = 4, 7, ...) tak, že sú pootočené a pohybujú sa nahor. Skutočnosť, že sa samoreprodukujúce štruktúry objavené použitím genetických algoritmov neočakávane líšia od predtým navrhnutých replikantov naznačuje, že ďalšie skúmanie v priestore možných samoreprodukujúcich sa štruktúr za použitia genetických algoritmov prinesie ďalšie nové štruktúry.