Prírodou inšpirované algoritmy

Langtonove Q-slučky

Prvé samoreprodukujúce sa celulárne automaty( Neumannov CA aj Coddov CA ) boli tvorené obrovským množstvom buniek. Zložitosť týchto modelov sa zdá byť zhodná s mimoriadnou zložitosťou biologických samoreprodukujúcich sa štruktúr. Naznačujú, že samoreprodukcia je prirodzene zložitý jav. Novšie práce o samoreprodukujúcich sa slučkách poskytujú dôkaz, že to tak vôbec nemusí byť.

Langton (Langton, 1984) zostrojil na báze Coddovho modelu neporovnateľne jednoduchšiu verziu samoreprodukujúceho sa 2D CA (rezignoval ale na emuláciu Turingovho stroja), tzv. Q-slučku (Q-loop, označovanú niekedy tiež ako SR-loop = Self Reproducing loop alebo SL86S8V). Táto samoreprodukujúca sa štruktúra, sa skladá z 86 buniek, z ktorých každá môže nadobúdať jeden z 8 možných stavov. Každá z buniek určuje svoj stav v nasledujúcom kroku zo stavov svojich štyroch susedov a zo svojho vlastného stavu. Preto počet všetkých možných pravidiel ktoré je možné pre túto štruktúru napísať, predstavuje 85=32768 pravidiel. V skutočnosti na riadenie reprodukcie slučky je potrebných iba 101 pravidiel. Tieto pravidlá však nepokrývajú celú komplexitu správania sa slučiek v kolónii takže počet všetkých potrebných pravidiel je 219. Pravidlá, ktoré sú na popis takejto samoreprodukujúcej sa slučky potrebné, sú obyčajne zapísane ako šestica čísel resp. symbolov (pre slučky s von neumannovským okolím). V tomto zápise pravidla predstavuje:

• prvé číslo alebo symbol aktuálny stav bunky v n-tom kroku
• druhé číslo alebo symbol stav severného suseda v n-tom kroku
• tretie číslo alebo symbol stav východného suseda v n-tom kroku
• štvrté číslo alebo symbol stav južného suseda v n-tom kroku
• piate číslo alebo symbol stav západného suseda v n-tom kroku
• šieste číslo alebo symbol stav, v ktorom sa bude bunka nachádzať v n+1 kroku

Označenie:
Farba	čierna	modrá	červená	magenta	zelená	cyan	žltá	biela
Číslica	0	1	2	3	4	5	6	7
Symbol	.	O	X	*	L	#	-	+

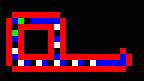
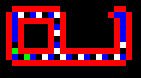
Na nasledujúcom obrázku je zobrazená Langtonova slučka. Ako je vidieť, vnútri slučky koluje informácia zložená z postupnosti dvojíc čísel 70 70 70 70 70 70 40 40.

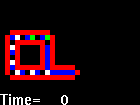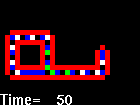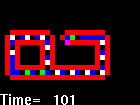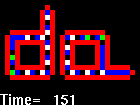
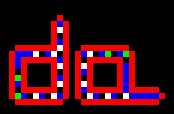
Táto informácia sa v mieste rozvetvenia zdvojí a postupuje okrem slučky aj do jej výbežku. Príchodom každej zo šiestich dvojíc 70 na koniec výbežku sa tento predĺži o jednu bunku (generácie 7, 11, 15, 19, 23 a 27) až nakoniec v generácii 34 sa po príchode čiastkovej informácie 40 40 sa rameno slučky stočí smerom doľava. Predlžovanie a stáčanie doľava sa zopakuje ešte dvakrát, až v kroku 120 sa uzavrie aj druhá slučka. V kroku 126 sa v spojnici dvoch slučiek objavia stavy 5 a 6. Stav 5 smeruje doľava a potom v obale smerom hore, až v kroku 137 iniciuje rast výbežku ľavej slučky smerom nahor. Stav 6 smeruje doprava ako súčasť "zdedenej" informácie 70 70 70 60 70 70 40 40 a v kroku 137 iniciuje rast výbežku pravej slučky smerom doprava (pri vetvení smerom nahor sa dvojica 60 mení na pôvodnú 70). Nakoniec je v kroku 151 proces samoreprodukcie ukončený.

Naznačený proces pokračuje ale ďalej a v generácii 301 už existujú štyri slučky, v generácii 451 je ich už osem. V prostrednej slučke dolného radu v tejto chvíli dochádza k postupnej deštrukcii "krúžiacej informácie" a táto slučka ani nemá priestor pre vytvorenie výbežku (proces zmienenej deštrukcie je završený v generácii 466). Toto postupné "odumieranie" vnútorných slučiek, nemajúcich dostatok priestoru, pokračuje ďalej a vzniká akási kolónia (pripomínajúca korálové útvary) slučiek, rastúcich na obvode a obklopujúca stále väcšie "mrtve" jadro.

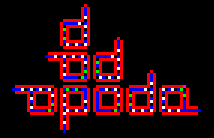Langtonove Q-slučky sú názornou ilustráciou dvojakej funkcie informácie:

• neinterpretovaná informácia (genotyp) sa kopíruje do potomka
• interpretovaná informácia (fenotyp) charakterizuje tvar a chovanie jedinca, teda tvar a veľkosť slučky

Langtonove slučky si môžete vyskúšať v applete.