Prírodou inšpirované algoritmy

Čo je to Celulárny Automat

Celulárny automat

Celulárny automat (ďalej označovaný aj ako CA) je dynamický systém, diskrétny v priestore aj čase. Je tvorený pravidelnou štruktúrou buniek v N-rozmernom priestore (najčastejšie je N=2, tzv. 2D CA, kde bunky tvoria štvorcovú mriežku). Každá bunka môže nadobúdať jeden z K možných stavov. Často sa jedná iba o dva stavy: 0-mŕtva bunka, 1-živá bunka; v tomto prípade sa občas stav 1 označuje ako bunka a 0 ako prázdne políčko (mriežky). Hodnoty stavov buniek v ďalšom časovom kroku (v nasledujúcej generácii) sa vypočítajú paralelne na základe lokálnej prechodovej funkcie (rovnakej pre všetky bunky). Argumentmi tejto funkcie sú aktuálne hodnoty stavov vyšetrovanej bunky a všetkých susedov (buniek v jej okolí). V prípade 1D CA je okolie charakterizované tzv. polomerom - počtom susedov po oboch stranách vyšetrovanej bunky; v prípade 2D CA tvoria okolie štyri priľahlé bunky (tzv. neumannovské okolie) alebo sa do okolia zaradia aj štyria ďalší susedia, dotýkajúci sa vyšetrovanej bunky len v rohoch (tzv. úplné okolie). Používa sa viacero druhov okolí z ktorých medzi najznámejšie patria:

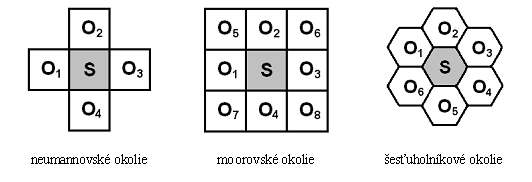
Lokálna prechodová funkcia f definujúca stav bunky v čase t+1 pre okolia na hore uvedenom obrázku, má tvar

Lokálna prechodová funkcia býva často definovaná sadou pravidiel, ktoré môžu byť zadané slovne (napríklad v prípade hry LIFE), prípadne graficky ( Margolusov biliardový automat).

Spravidla sa predpokladá, že štruktúra buniek je nekonečná. V praktických realizáciách sa buď predpokladajú okrajové bunky identicky za nulové (prázdne), alebo sú okraje "prepojené" a tvoria v prípade 1D slučku a v prípade 2D anuloid. Niektoré z K možných stavov sú označované za kľudové; keď bunka v kľudovom stave má vo svojom okolí tiež iba bunky v kľudovom stave, potom sa hodnota jej stavu v ďalšej generácii nemení.
Niekedy je účelná širšia koncepcia, v ktorej sú pre CA charakteristické tri kľúčové vlastnosti:

• paralelizmus (výpočet nových hodnôt stavov všetkých prvkov prebieha súčasne, na bežných sériových počítačoch sa musí tento postup simulovať)
• lokalita (nový stav prvku závisí len na jeho pôvodnom stave a na pôvodných stavoch prvkov z jeho okolia)
• homogenita (pre všetky prvky platí rovnaká prechodová funkcia)

CA môžu slúžiť ako vhodné modely nielen pre biologické ale aj fyzikálne a spoločenské procesy. Každá živá bunka, každý element, každý jedinec totiž mení svoj stav súbežne s ostatnými (paralelizmus), v závislosti na stave svojho okolia (lokalita) a na základe rovnakých zákonitostí (homogenita).