Prírodou inšpirované algoritmy

Úvod

Čo sú to fraktály?

Na fraktály sa môžeme pozrieť dvoma pohľadmi. Pri tom prvom za fraktál považujeme obrazec alebo prírodný vzor. Takýchto fraktálov je v prírode nespočetné množstvo, za všetky spomeňme napríklad kôru stromov, alebo žilky na listoch stromov. Ten druhý pohľad na fraktály má čo to dočinenia s geometriou. Ide o obrazce, ktoré vznikli v počítači na základe vopred daných algoritmov. Jeden z nich si popíšeme nižšie.

Čo sú to Voronoiove diagramy?

V jednoduchosti povedané, Voronoiov diagram je súhrn čiar okolo vopred daných hlavných (main) bodov na nejakom vopred danom území. Tieto čiary tvoria hranice medzi hlavnými bodmi tak, že pre každý iný bod z územia vytýčeného deliacimi čiarami platí, že zo všetkých vzdialenosti k hlavným bodom, je najkratšia vzdialenosť k tomu hlavnému bodu v území akého sa práve nachádza. Alebo inak povedané, deliace čiary tvoria body, ktorých najbližšia vzdialenosť od nejakého hlavného bodu je rovnaká pre minimálne dva rôzne hlavné body.

Čo sú to rekurzívne Voronoiove diagramy?

Najlepšie bude vysvetliť si túto rekurziu v niekoľkých krokoch.

1. Máme ohraničenú plochu.
2. Na danú plochu vložíme zopár bodov, ktoré budú v nasledujúcom kroku hlavné body.
3. Vytvoríme Voronoiov diagram okolo hlavných bodov na každej ohraničenej ploche.
4. Deliace čiary nám vytýčili nové ohraničené plochy a do týchto plôch znovu vložíme body, ktoré budeme pri ďalšej tvorbe Voronoiovych diagramov považovať za hlavné. Body pomocou ktorých boli vytvorené deliace čiary ohraničených plôch už neberieme do úvahy.
5. Rekurzívny návrat na 3.krok.

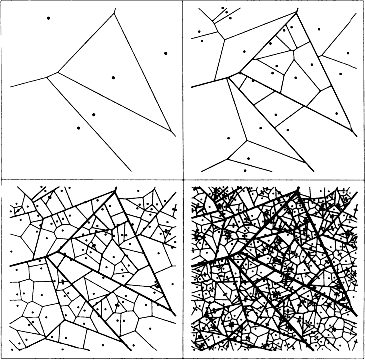
Tento postup je podrobnejšie opísaný v nasledujúcej podkapitole. Takýmto postupom vytvoríme fraktály za použitia Voronoiovych diagramov. Pre lepší výsledný efekt sú generačne najstaršie deliace čiary najhrubšie. Pre zvyšné generácie sa deliace čiary postupne stenčujú. Pomocou tejto metódy môžu vzniknúť obrazce pripomínajúce listy(hranice sú žilky listov), autoatlas(diaľnice, hlavné cesty, vedľajšie cesty), mapy(napr. hranice štátov, krajov, okresov, obcí).

Čo je to Voronoiov mnohosten?

Ide o trojrozmernú podobu Voronoiovych diagramov pri ktorých sú body umiestnené v trojrozmernom priestore a namiesto deliacich čiar sú body od seba separované deliacimi rovinami. Takýto mnohosten vidíme aj na nasledujúcom obrázku.

Čo sú to Delaunayove diagramy?

Delaunayov diagram je trojuholníková mriežka na množine vrcholov s vlastnosťou, že žiadny vrchol z množiny vrcholov nepatrí do vnútra kružnice vpísanej ľubovoľnému trojuholníku z trojuholníkovej mriežky. Pre lepšiu predstavu doporučujem pozrieť si Applet#3.