Prírodou inšpirované algoritmy

Bifurkačný diagram

Charakter iteračného procesu sa výrazne mení v závislosti od hodnoty r, označovanej ako biotický potenciál. Môžeme pritom pozorovať tri režimy správania:

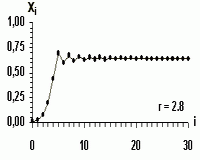
1. ustálenie na konštantnej hodnote
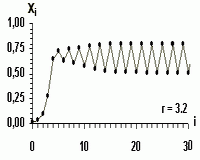
2. ustálenie na periodických kmitoch
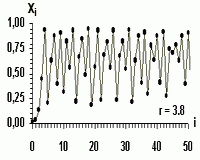
3. chaotické správanie (ale nevybočujúce z istého intervalu hodnôt).

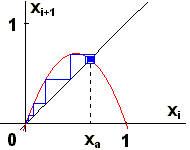
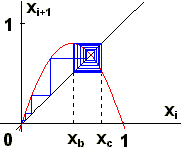
Sledovanie iteračného procesu uľahčia tzv. cobweb diagramy (cobweb - pavučina), ktoré predstavujú grafické riešenie sústavy dvoch rovníc: xi+1 = rxn(1-xi) a xi = xi+1.

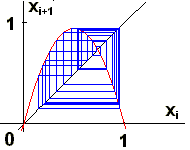V prvých dvoch prípadoch východzia hodnota x0 ovplyvní síce prechodový dej, ale ustálený režim je už na x0 nezávislý. Naznačené typy správania znázorňuje tzv. bifurkačný diagram (BD) v koncentrovanej grafickej podobe. V ňom sa pre všetky hodnoty 0 < r ≤ 4 na vodorovnej ose vynášajú v zvislom smere hodnoty xi po doznení prechodových dejov. Pre jednotlivé r dostaneme potom podľa príslušného typu správania:

1. jeden bod - ustálenie na konštantnej hodnote); pre 0 < r ≤ 1 sa xi ustáli na nule, teda populácie vyhynie - na obrázku je táto časť vynechaná.
2. n bodov pre periódu n ustálených kmitov
3. chaoticky rozložené body na úsečke.

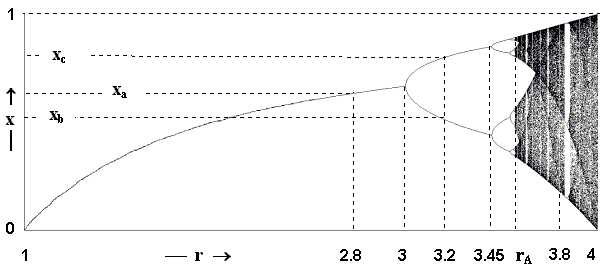
Na nasledujúcom applete je možné sledovať, ako sa mení dynamika iterácie v závislosti na voľbe hodnoty r. Radiobuttonmi je možné navoliť niektoré charakteristické režimy ale je možné jazdcom pod pravým oknom voliť aj iné r. Jazdcom pod ľavým oknom je možné voliť východziu hodnotu x0.

1. ustálenie na konštantnej hodnote
1. vyhynutie - pre 0 < r ≤ 1 smeruje hodnota xi s rastúcim i k nule, teda populácie vyhynie,
2. aperiodické ustálenie na nenulovej hodnote - pre 1 < r ≤ 2 je prechodový dej monotónny (bez prekmitu),
3. kmitavé ustálenie na nenulovej hodnote - pre 2 < r ≤ 3 dochádza k prekmitnutiu a prechodový dej predstavuje tlmené kmity. Napríklad pre r = 2.8 sa tieto kmity ustália na hodnote xa= 0.6429.
2. oblasť bifurkácií - Pri hodnote r = 3 nastáva bifurkácia (delenie krivky na dve vetvy - odtiaľ aj názov diagramu). Pre 3 < r < 1+√6 =3.44949... vzniknú po doznení prechodových dejov kmity s periódou 2, napr. pre r = 3.2 sú to hodnoty xb = 0.5130 a xc = 0.7995. Pri hodnote r = 1+√6 ≅3.45 dochádza k ďalšej bifurkácii - objavia sa kmity s periódou 4. Ďalší rast r je sprevádzaný novými a novými bifurkáciami a teda aj ďalším zdvojovaním periód. Proces postupných bifurkácií končí pri hodnote rA = 3.569945672... (v tzv. akumulačnom bode), za ktorým začína oblasť chaosu.
3. oblasť chaosu
1. chaotické správanie - iteračný proces predstavuje nepravidelnú postupnosť hodnôt z určitého intervalu (resp. niekoľkých neprekrývajúcich sa intervalov,
2. okná vyšších periód s vnorenými bifurkáciami - ustálenie na kmitoch s vyššími periódami, napr. pri hodnote r = 1+√8 ≅3.83 začína okno cyklov s periódou 3, konkrétne pre r = 3.84 ho predstavujú hodnoty x = 0.1493, 0.4877 a 0.9594. Sú tu aj okná pre cykly s periódou 5, 6. 7, ... , pričom aj v týchto oknách dochádza k bifurkáciám.

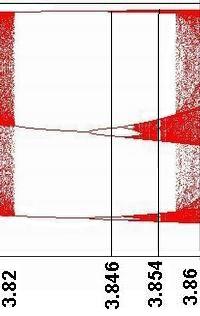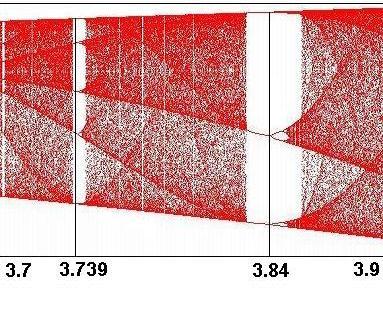
Predchádzajúci obrázok v ľavej časti prezentuje výrez BD s už spomínaným oknom periódy 3 ako aj okno pre cyklus s periódou 5, ktoré začína pri r = 3.73817. Aj v týchto oknách dochádza k bifurkáciám - základná perióda sa na pravom okraji okien opakovane zdvojuje. Pravá časť predošlého obrázku znázorňuje detailnejšie okno periódy 3, v ktorom je pre hodnotu r = 3.846 kúsok za bifurkáciou perióda 6. Na konci okna nastáva zase chaos aj s "vnorenými" oknami vyšších periód (napríklad pri r = 3.854 perióda 9 ako analógia okna periódy 3 v pôvodnom BD).

Uvedené výrezy naznačujú, že BD vykazuje fraktálový charakter - kvázi-sebapodobnosť na rôznych úrovniach. Nakoľko pri týchto výrezoch došlo iba k redukcii horizontálneho rozmeru BD, spomínaná kvázi-sebapodobnosť nie je dobre viditeľná. Nasledujúci applet je z tohoto pohľadu oveľa názornejší.

Applet je rozdelený do troch okien. Po jeho spustení je v prvom okne vykreslený bifurkačný diagram a v ňom je sivým štvorcom vyznačená oblasť pre zoomovanie. Stredné okno zobrazuje túto oblasť v 8 násobnom zväčšení. Aj v ňom je ďalším sivým štvorcom vyznačená oblasť pre zoomovanie. Tretie okno potom zobrazuje túto oblasť v 52 násobnom zväčšení vzhľadom k prvému oknu. V treťom okne je možné opakovane vyznačiť myšou ďalšie výrezy. Pôvodný obsah tretieho okna je potom prekresľovaný do druhého a v treťom je vykreslený nový zväčšený výrez. V druhom okne je sivým štvorcom naznačená časť bifurkačného diagramu, ktorá je vykreslená v treťom. V prvom okne sú z dôvodu prehľadnosti vykresľované už len vodiace čiary, kde stred aktuálneho (posledného) výrezu je v ich priesečníku.

Po kliknutí na Reload je vykreslený bifurkačný diagram len v prvom okne (druhé a tretie sú prázdne).Zároveň je prvé okno aktívne, čiže je v ňom možné urobiť výrez (len štvorcový). Následne bude výrez z prvého okna vykreslený v druhom okne pod ktorým sa nachádza aj hodnota jeho zväčšenia. Teraz je aktívnym druhé okno v ktorom obdobne môžeme vyznačiť výrez, ktorý bude vykreslený v treťom. Ďalej už pokračujeme spôsobom, opísaným v predchádzajúcom odstavci.

V (Yorke a Li, 1975) je uvedený dôkaz, že keď sa v ľubovolnom jednorozmernom systéme objaví pravidelný cyklus s periódou tri, potom bude vykazovať aj cykly s vyššími periódami a tiež aj úplne chaotické úseky.