Prírodou inšpirované algoritmy

Prehľad appletov na webe

Applet	Popis appletu
	Tento applet umožňuje zobrazenie diffúzno-reakčného systému, pričom ma možnosť využívať už prednastavené hodnoty premenných, ktoré sa taktiež dajú meniť manuálne( zmena farieb, rýchlosť a obsah inhibítorov a agentov). http://texturegarden.com/java/rd
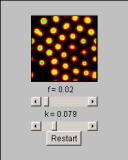	Jednoduchý applet vykresľujúci reakciu medzi dvoma chemikáliami U a V, pričom U difunduje rýchlejšie než V. Dynamika je popísaná opäť diferenciálnymi rovnicami, pričom samotný systém umožňuje vykresľovanie rôznych vzorov napr. vĺn, labyrintu atd. http://www.design.chalmers.se/people/joakim_linde/ java/ReactionDiffusion/reactiondiffusion.html
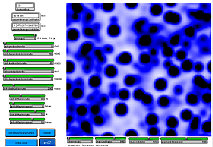	V hornom rohu appletu sú tri sledovacie okná kde sa zobrazuje momentálny počet aktivátorov a inhibítorov. Pod oknami sa nachádza niekoľko nastavení umožňujúcich meniť koeficienty rovníc pre inhibítory, aktivatory, rýchlosť difúzie a reakciu dvoch látok. http://zool33.uni-graz.at/schmickl/Self-organization/ Pattern_formation/Reaction-diffusion/ reaction-diffusion.html
	Jednoduchý applet reakčno-difúznej rovnice pre zvolené parametre má systém 2 jednoznačné stavy (biely a červený), počiatočný prúžok sa postupne rozvetví a zapĺňa oblasť labyrintovým vzorom. http://cnls.lanl.gov/~aric/Simulations/Labyrinth/Java/
	Applet zobrazuje dve okná, zobrazujúce koncentráciu inhibítorov a aktivátorov v čase. Ďalšie nastavenia appletu umožňujú meniť v diferenciálnych rovniciach koeficienty difúzie aktivátorov a inhibítorov, počiatočné podmienky, farbu koncentrácie. http://www.csa.ru/Inst/gorb_dep/inbios/genet/ Netmodel/patform/aplet.htm"
	Tento reakčno-difúzny systém je použitím CA, ktorý sa pri spustení nastaví rôzne (náhodne) na čiernu a bielu farbu. Po niekoľkých generáciách bunky CA začnú vytvárať vzory viditeľné na zvieratách s pruhmi zebry a tigre. V samotnom applete nie je možné nič nastavovať. !!! Upozornenie: Applet po natiahnutí spôsobuje enormné využitie CPU !!! http://grace.evergreen.edu/artofcomp/examples/ zebra/Zebra.html
	Jednoduchý applet modelujúci reakčno-difúzny systém. Obsahuje 16 moźných výsledných śtruktúr. Podĺa autora je jeho ovládanie intuitívne. http://hometown.aol.com/jiweichsel/wr3.html
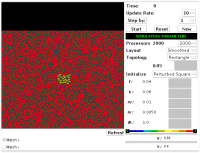
	Zaujímavá simulácia Gray-Scott-ovho RD modelu. Užívateľovi dáva možnosť nastavovať všetky parametre simulácie (F, k, Du, Dv a časový krok), ďalej vybrať si usporiadanie a počet buniek (autori ich označujú ako procesory) na mriežke, tvar mriežky a polomer oblasti, ktorú každá bunka ovplyvňuje. Dá sa sledovať časový priebeh koncentrácie, no vždy len jedného reaktantu (z dvoch možných). Kliknutím na bunku sa zobrazia jej informácie. Na strámke je spolu s appletom aj dosť kvalitný popis ovládania a všetkých jeho funkcií. http://www.swiss.ai.mit.edu/projects/amorphous/jsim/sim/GrayScott.html
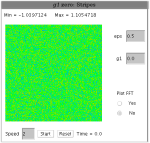
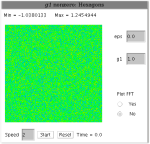
	Applet simuluje dynamický systém popísaný Swift-Hohenberg-ovou rovnicou. Demonštruje všeobecný a dôležitý princíp: ak dynamická rovnica nie je symetrická, tak pre malé epsilon vznikajú vzory pripomínajúce šetsťuholníky. Na druhej strane, ak je v rovnici zachovaná symetria vnikajú obrazce pripomínajúce pruhy (resp. štvorce, obdĺžniky). SH rovnica je symetrická pre hodnotu parametra g1 = 0.0, nenulový parameter poruší symetriu. Skladá sa z dvoch okien. V prvom sa dá spustiť simulácia s vopred nastavenými parametrami na hodnoty: epsilon = 0.5 g1 = 0.0 V druhom okne má simulácia nastavené parametre na hodnoty: epsilon = 0.0 g1 = 1.0 Je tu možnosť nastaviť rýchlosť simulácie, parametre a zvoliť vykresľovanie Fourierovej transformácie. http://www.cmp.caltech.edu/~mcc/STChaos/SH.html
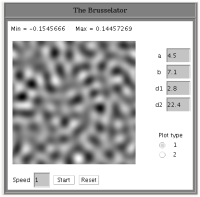	Applet využíva sústavu parciálnych diferenciálnych rovníc, pričom je možné v týchto rovniciach nastavovať premenne a a b, ktoré by mali predstavovať koncentráciu morfogénov. Je možné nastaviť aj d1 a d2 parametre použite v sústave týchto rovníc. Sústava popisuje zmeny týchto koncentrácií v čase. http://www.cmp.caltech.edu/~mcc/STChaos/ Brusselator.html
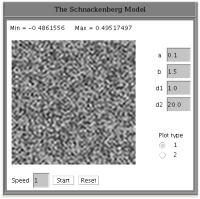
	Tento applet je takmer rovnaký ako vyššie uvedený "Brusselator". Jediný rozdiel je v použitej sústave rovníc, ktorá popisuje dynamiku systému. http://www.cmp.caltech.edu/~mcc/STChaos/Schnackenberg.html