Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Gravitačný stroj katastrof
Podkapitoly:
Applet
Stroj pozostáva z dvoch kúskov tenkého oceľového plechu parabolického tvaru pospájaných tenkými a krátkymi drôtmi. Malý silný magnet uchytený na prednom plechu môže byť posúvaný do hociktorej požadovanej polohy bez toho, aby zdeformoval konštrukciu. Keďže väčšina hmotnosti takto poskladaného zariadenia je obsiahnutá v magnete, môžeme povedať, že polohu ťažiska predstavuje pozícia magnetu. Ak je stroj položený na vodorovnej ploche, ťažisko sa snaží dostať kolmo nad dotykový bod s touto plochou. Ak je plocha šikmá, konštrukcia zaujme polohu takú, že ťažisko bude ležať na normále tejto plochy.
Touto problematikou sa aktívne zaoberá Lucien Dujardin a práve na základe jeho tutoriálom catastrophe teacher je inšpirovaná celá kapitola.
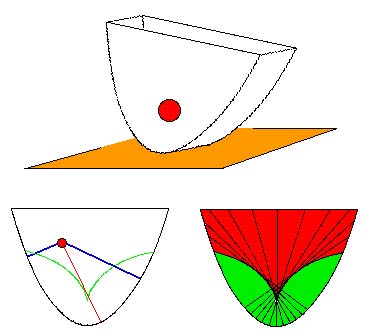
Gravitačný stroj katastrôf (podľa L.Dujardina)
Gravitačný stroj katastrofy je typu hrot teda vychádzame z potenciálovej funkcie štvrtého rádu. Keďže ide o fyzikálny systém tak potenciálovú funkciu (na rozdiel od príkladu so zmenami farby) reprezentuje skutočná potenciálna energia
P = m * g * h
Predpokladajme, že
m * g = 1
potom celá potenciálna energia je rovná h , čo je vlastne vzdialenosť polohy ťažiska
v parabole (kolíske) od dotykového bodu paraboly s plochou, po ktorej sa parabola
odvaľuje (na obrázku vľavo je táto vzdialenosť znázornená modrou úsečkou). Majme parabolu definovanú ako
y = 2x2
potom potenciálová funkcia bude reprezentovaná euklidovskou vzdialenosťou polohy ťažiska a dotykového bodu s dosadením rovnice paraboly, čiže
V(x) = (x - a)2 + (y - b)2
V(x) = (x - a)2 + (2x2 - b)2
V(x) = 4x4 + (1 - 4b)x2 - 2ax + a2 + b2
kde a, b reprezentujú polohu ťažiska v parabole. Pre určenie stavu polohy ťažiska,
kde bude mať parabola dva stabilné stavy a kde jeden stabilný stav, slúži bifurkačná krivka
(na obrázku vľavo znázornená zelenou čiarou). Ak sa ťažisko nachádza v zelenej zóne na obrázku vpravo,
bude mať parabola len jeden stabilný stav, čiže po naklonení paraboly z tohoto
stabilného stavu a nasledovnom uvolnení sa parabola preklopí späť do tohoto stavu.
V prípade nastavenia polohy ťažiska do červenej zóny bude mať parabola 2 stabilné
stavy. V prípade naklonenia paraboly a nasledovnom uvolnení sa parabola ustáli
v najbližšom stabilnom stave.
Výpočet bifurkačnej krivky má obecný charakter pre všetky typy katastrôf. Vychádzame z potenciálovej funkcie. Urobíme jej deriváciu. Z derivácie vypočítame diskriminant. Diskriminant položíme rovný nule a vyjadrením dostaneme rovnicu bifurkačnej krivky. Derivácia potenciálovej funkcie je nasledovná
V'(x) = 16x3 + 2(1 - 4b)x - 2a
Diskriminant teda v našom prípade bude vyzerať nasledovne
D3 = [(4b - 1)3 / 128] - (27a2 / 64)
Z toho ľahko vyjadríme rovnicu bifurkačnej krivky
b = 1/4 + (3/2)*(a2/4)^(1/3)
Aplikačný potenciál gravitačného stroja katastrôf je napríklad pri správnom navrhovaní trupov lodí ako aj rozložení materiálu v nich. V prípade zlého navrhnutia budú mať dva stabilné stavy pričom jeden z nich môže byť prevrátenie lodi.
