Prírodou inšpirované algoritmy

Parametrické L-systémy

V tomto príklade si podrobnejšie rozoberieme parametrické L-systémy. Ako je zrejme z predošlých príkladov pridaním vlastností ako: vetvenie, náhodnosti a kontextovej senzitivity sa možnosti využitia L-systémov podstatne rozšírili. No napriek týmito novým vlastnostiam sme boli stále obmedzený na preddefinovaný uhol a konštantnú dĺžku posunu korytnačky pri kreslení obrazca, čo je pre generovanie niektorých štruktúr nedostačujúce, alebo to znamená zväčšenie zložitosti a neprehľadnosti zápisu L-systému. Parametrické L-systémy boli navrhnuté hlavne pre odstránenie týchto nedostatkov a taktiež na ďalšie rozšírenie možností použitia formalizmu L-systémov v simuláciách. Ako základnom pri týchto L-systémoch je zavedenie číselného parametra pre symboly pohybu korytnačky a jej natočenia, t.j. parametra určujúceho veľkosť posunu resp. natočenia. K tomu sa ďalej pridávajú parametre ovplyvňujúce napr. farbu čiar, hrúbku čiar, ich inkrementáciu a pod. Ďalšou vlastnosťou parametrických L-systémov je používanie symbolických parametrov a doplnenie pravidiel o podmienkovú časť, ktorá je tvorená logickým výrazom, obsahujúcim formálny parameter. Potom môžu jednému prepisovaciemu pravidlu prislúchať viaceré pravidlá s disjunktnými podmienkovými časťami. Čiže výber pravidla je podmienený splnením jeho podmienkovej časti dosadením hodnoty skutočného parametra prepisovaného symbolu. Poďme si ale parametrické L-systémy predstaviť priamo na príklade. Otvoríme si nový projekt, môžete, ale nemusíme použiť štandardné parametre v sekcii View. V sekcii L-system zadajme nasledujúci L-systém.

#define STEPS 7
#define a 86
#define p 0.3
#define q (1-p)
#define h ((p*q)^0.5)
lsystem: 0
derivation length: STEPS
axiom: -(90)F(1)
F(x) : x > 0.05 --> F(x*p) + (a)F(x*h) - (a+a)F(x*h) + (a)F(x*q)
endlsystem

A spusťme simulátor cpfg! Dostávame nasledujúci výstup:

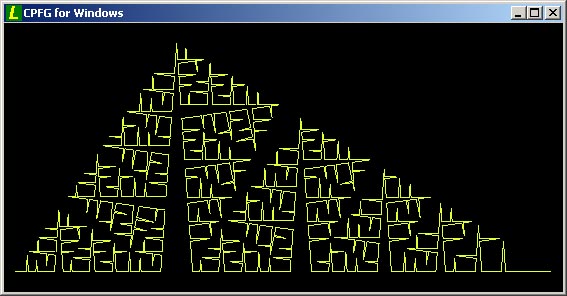
Pozrime sa teraz na tento príklad bližšie. Pre názornosť vychádzajme z obrázka:

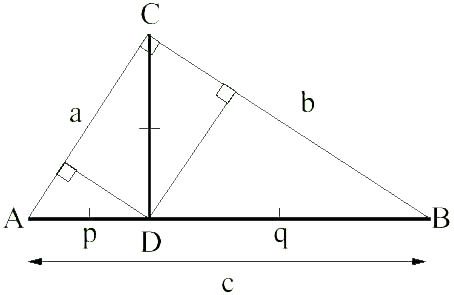
Tento L-systém využíva parametre pre kontrolu posunu korytnačky ako aj jej natočenia. Názorne je to vidieť v definícii axiómy: -(90)F(1): v prvej zátvorke je parameter natočenia korytnačky a v druhej je to parameter posunu. Ako základ pre generovanie L-systému je použitá prepona AB, trojuholníka ABC, čo odpovedá už spomenutej axiómy. V následnom generovaní je úsečka AB rozdelená na segmenty AD a DB, čo odpovedá prvej a štvrtej hrane pravidla:

F(x) : x > 0.05 --> F(x*p) + (a)F(x*h) - (a+a)F(x*h) + (a)F(x*q)

Zatiaľ čo zvyšné dve hrany (t.j. druhá a tretia) smerujú takmer kolmo na hor v smere úsečky CD, ktorá je v podstate výškou daného trojuholníka. Takmer, preto, lebo parameter natočenia a nadobúda hodnotu 86. Hodnotu výšky h a zvyšnej časti q, určíme pomocou elementárnej geometrie:

p = q - c;
h = sqrt(p*g)

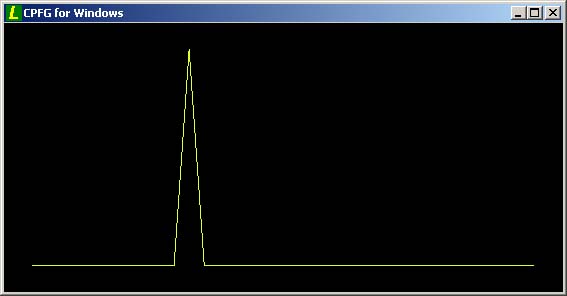
Pre názornosť po prvom derivačnom kroku dostávame nasledujúci obrazec:

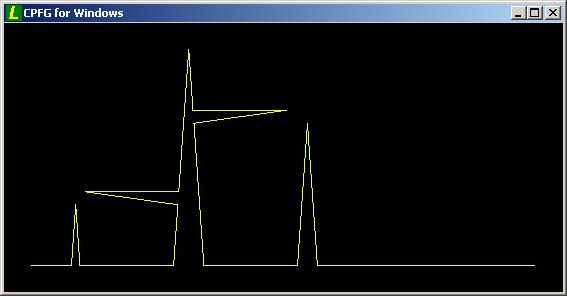
V ďalšom kroku, sú tieto štyri hrany stotožnené s preponami štyroch trojuholníkov vo vnútri trojuholníka ABC, potom dostávame:

Parameter x je obmedzený na dĺžku x > 0.05 po zmene na x > 0.005 a zvyšný derivation length na 10 dostávame: