Prírodou inšpirované algoritmy

Aplikácie DLA & FDS

Fraktálové modely DLA (difúzne ohraničené zhlukovanie) sa využívajú najmä v počítačovej grafike na simuláciu rastu rastlín, koralov, machov a rôznych iných prvkov živej a neživej prírody. Modely FDS (fraktálové drenažné systémy) sa používajú na simuláciu rôznych prírodných povrchov, spojenú so zobrazovaním erózie pôdy. Okrem grafických simulácií nás tieto modely tiež inšpirujú k riešeniu kombinatorických problémov, ako je to pri probléme obchodného cestujúceho.

Riešenie problému obchodného cestujúceho

Cesta obchodného cestujúceho patrí do triedy "NP - úplných problémov". To znamená, že tento problém nemôže byť exaktne vyriešený v lepšom ako polynomiálnom čase. Problém môžeme popísať následovne: Máme množinu miest spolu s množinou vzdialeností každého páru miest. Mestá reprezentujú body na nejakej rovine a máme za úlohu prejsť všetky mestá tak, aby prejdená vzdialenosť bola minimálna, každé mesto sme navštívili iba raz a vrátili sa do štartovacieho bodu. Mestá predstavujú uzly grafu a cesty medzi nimi hrany.

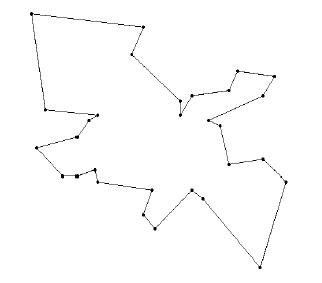
Grafová reprezentácia cesty obchodného cestujúceho

Na riešenie tohto problému existuje veľa heuristík. Medzi najznámejšie patria Lin a Kernighanov algoritmus (Lin a Kernighan, 1973), elastická sieťová metóda (Durbin a Willshaw, 1987), metóda najbližších susedov (Telfar, 1994), ako aj riešenie pomocou genetických algoritmov(Goldberg 1989, Zbigniew 1994). Časová zložitosť najlepšieho algoritmu Usamiho Yoshiyukiho a Kanoa Yoshikiho je T(n) = O(N*log(N))2 (Yoshiyuki a Yoshiki, 1995).

Moreno a Santos (Santos a Moreno, 1998) použili metódu DLA na riešenie problému cesty obchodného cestujúceho v euklidovskom priestore.

DLAH – DLA based heuristic

Základnou myšlienkou tohto algoritmu je spustenie N dvojrozmerných simulácií, kde N je počet miest (použitie celulárnych automatov a bitových operátorov) na štvorcovej mriežke. Pozície semiačok korešpondujú s pozíciami miest. Tento model necháme rásť a tam, kde sa dva agregáty spoja (prekrížia), dochádza k prideleniu cesty. Prebieha to až pokým nenastanú lokálne cykly. Ak nastane prípad prekríženia viac ako dvoch agregátov, dochádza k spúšťaniu lokálneho náhodného procesu – "rulety". Ak mesto získalo dve hrany – rast agregátu je zastavený. V prípade, že každé mesto dosiahlo stav dvoch hrán, získavame riešenie.

Z výsledkov, ktoré dosiahli Moreno a Santos vyplynulo, že riešenie problému obchodného cestujúceho metódou DLA dáva lepšie výsledky ako riešenie tohto problému pomocou metódy najbližších susedov.

Inštancia o veľkosti 10 miest

Riešenie problému A pomocou DLA