Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Teoretické prístupy k DLA
Bohatosť DLA prirodzene prilákalo mnoho teoretických pokusov o komplexnú analýzu týchto zhlukov. Najväčšou prekážkou je absencia jednoducho identifikovateľného malého parametra, ktorý by umožnil analýzu odchýlok. Vyzerá to tak, že zhluky DLA uprednostňujú fraktálne štruktúry, v ktorých sú fluktuácie dôležité a nemôže byť u nich použitá teória stredného poľa (mean-field theory).
Prístup Hastingsona-Levitova
Hastings a Levitov vytvorili elegantnú reprezentáciu rastu DLA ako problém v iterovaných konformných mapách (Hastings a Levitov, 1998). Ich formulácia oživila záujem o problém DLA vytvorením silných nástrojov analytickej teórie funkcií, ktoré by popisovali tento fenomén.
Predstavme si zhluk o n časticiach. Riemannova mapovacia teoréma nás ubezpečuje, že existuje konformná mapa w = Fn(z), ktorá mapuje kruhový útvar v komplexnej z-rovine na povrch zhluku vo fyzickej w-rovine. Ak vonkajšok kruhového útvaru je namapovaný na vonkajšok zhluku, potom Fn je acyklická funkcia na vonkajšku kruhového útvaru. Konformálne mapovanie potom hovorí, že uhlová vzdialenosť medzi dvoma bodmi na kruhovom obvode v z-tových súradniciach je úmerná celkovému nárastu pravdepodobnosti pozdĺž oblúku, ktorý je spojený obrazcami týchto dvoch bodov vo fyzickom priestore.
Predstavme si mapu w = Fn(z), ktorá mapuje kruh v rovine z (modrá), na zhluk s n-časticami v rovine w (ružová). Mapa, ktorá zodpovedá zhluku s (n + 1) časticami nie je vytváraná pomocou mapovania kruhu, ale pomocou mapovania kruhu s "hrčou" f(z), ktorá je na nejakej pozíci θ pred premapovaním novej častice s rozmerom λ.
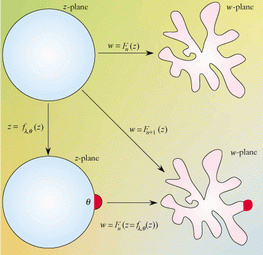
Hastingsova-Levitovova konformná iterovaná mapa

Kvázy periodický rast zhluku pomocou Hastingsova-Levitovova
Teória strún a DLA
Prekvapivo najviac sa rozvíjajúcim nápadom v poslednej dobe je istá možnosť vzťahu medzi Hele-Shawovým rastom a teóriou strún. Počiatočným okamihom pre toto rozvíjanie je pozoruhodný fakt, že Hele-Shawov rast v sebe uchováva harmonické okamihy vonkajších domén. Tieto momenty môžeme definovať pomocou
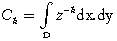
Kde integrujeme cez vonkajšok rastúcej štruktúry, z = x + iy je bežná komplexná premenná a divergencie vo vnútri integrálu sú primerane usporiadané. Co sa mení podobne, ako pri vzore rastu pomocou Hele-Shawa, ale ostatné Ck sú zafixované počas rastu. Problém určovania vzorov vytvorený Hele-Shawovým rastom je príbuzný problému určovania rodín slučiek s rôznymi hodnotami Co a s ostatnými pevnými hodnotami Ck.
