Prírodou inšpirované algoritmy

DLA, fraktály a multifraktály

DLA zhluky patria medzi najviac študované fraktálové objekty. Dimenzia fraktálu D spája počet častíc n s rozmerom r jedného zhluku: n = rD. V dvojrozmernom priestore je vidno, že D je približne 1,71 a v trojrozmernom priestore je D približne 2,5.

Napriek tomu, že v dvojrozmernom priestore bolo DLA najviac preštudované, je fraktálový pôvod kuriózne nestály. Napríklad fraktálová dimenzia je závislá na štruktúre mriežky. Keď sa uskutočňuje náhodný pohyb a rast zhluku sa deje na ploche, kde jednotlivé častice nezávisia na žiadnej mriežke, podľa ktorej by sa pohyb uskutočňoval, môžeme dostať D = 1,71. Keď budeme riešiť ten istý problém na štvorcovej mriežke, dosahuje D pre rozsiahle zhluky až hodnoty 3/2.

Zdá sa, že fraktálny rozmer DLA len málo závisí od geometrie simulácie. Výsledok D = 1,71 je dosahovaný pre radiálny rast zo štartovacieho bodu – semiačka. Pre rast z povrchu alebo pre rast v kanály môžeme dostať výsledok blízky D = 1,67 a malú, ale robustnú diferenciu líšiacu sa od prípadu radiálneho rastu. Zdá sa, že diferencia pokračuje po limit asymptotického rastu. DLA zhluky taktiež prejavujú multifraktalitu – vlastnosť pravdepodobnosti rastu na povrchu zhluku. Vezmime si zhluk s n časticami. I-tá častica má nejakú pravdepodobnosť pi, ktorá vraví o pravdepodobnosti uchytenia náhodne sa pohybujúcej častice. Pravdepodobnosti sú distribuované v širokej miere, od relatívne veľkých na vonkajších vrcholoch zhluku, po veľmi malé, ktoré sú v hĺbke fjordov. Preto je prirodzené merať mieru rozloženia tejto pravdepodobnosti. Môžeme definovať škálovaciu funkciu δ(q) ako exponent.

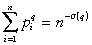
Prítomnosť netriviálnej funkcie q(g) vedie k multifraktalite.

• Zdroj