Prírodou inšpirované algoritmy

Hele-Shawov tok

V pórovitom prostredí je rýchlosť roztoku úmerná gradientu tlaku.

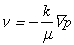
, kde k je permeabilita v priepustnom médiu a µ je viskozita tekutiny.

Ak je tekutina nestlačiteľná, pomocou divergencie prvej rovnice dostávame Laplaceovu rovnicu:

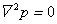
Dajme tomu, že do podobnej tekutiny vstrekneme ďalšiu tekutinu, ktorá sa s prvou nezmieša a bude mať oveľa menšiu viskozitu. Dostávame Hele–Shawovo prúdenie (Saffman a Taylor, 1958). Najlepším príkladom je vstrekovanie vody do vysoko viskózneho oleja v pórovitej hornine (napríklad pieskovci), ktorá je použitá pri druhotnom získavaní oleja. Kvôli nízkej viskozite môžeme tlak vstrekovaného roztoku nahradiť konštantou. Potom tok roztoku, ktorý má väčšiu viskozitu, je určený druhou rovnicou s konštantnou hranicou tlaku a jeho rýchlosť je určená pomocou prvej rovnice, ktorá taktiež určuje rýchlosť styčných bodov oboch roztokov.

Vstrekovanie roztoku s nízkou viskozitou (vody, zafarbenej na tmavo) do vysoko viskózneho hydrofóbneho roztoku viedlo k tejto rozmazanej verzii DLA z kapitoly Základný koncept.

Hele-Shawov tok

Je pozoruhodné že matematický popis týchto dvoch problémov (Hele-Shawov tok, DLA) je skoro identický. Pre Hele-Shawov tok, tlak spĺňa Laplaceovu rovnicu s hranicou konštantného tlaku a rýchlosť roztokov v mieste, kde sa spájajú, je úmerná gradientu tlaku. Pri DLA, pravdepodobnosť zahustenia náhodne chodiacej častice spĺňa Laplaceovu rovnicu s konštantnou pravdepodobnosťou zahustenia povrchu zhluku. V tomto prípade pravdepodobnosť rastu (a nie rýchlosť rastu) na povrchu je daná gradientom pravdepodobnosti zahustenia. Preto je DLA stochastická verzia Hele-Shawovho problému.

V koloidnej agregácii častice difundujú, kým v Hele-Shawovom toku ich tlak tekutiny rozptyľuje. V oboch prípadoch je nárast styčnej plochy dostatočne pomalý, takže sa radšej používa Laplaceova rovnica na modelovanie rozptyľovania. To naznačuje, že Laplaceov model môže byť nápomocný pri problémoch formovania základných vzorov, kde rozptýlený transport riadi rast štruktúry. Sú to prípady, kde bola použitá DLA alebo nejaká variácia DLA na modelovanie určitého fenoménu, ako je usporadúvanie povrchu pri mikroskopickom iónovom lúči, rozpade dielektrika, elektrodepozícii.

Minerálne dendridy

Vzorka oxidu mangánu na povrchu tohto kameňa je podobná obom simuláciám DLA kvalitatívne aj kvantitatívne.

• Zdroj