Prírodou inšpirované algoritmy

Kochova snehová vločka - začíname

V tomto prvom príklade sa pustíme do jednoduchého L-systému, ktorého výstupom bude obrazec veľmi podobný snehovej vločke. Patrí k najznámejším fraktálom autorom ktorého je Helga Koch. Prv než začneme, patrilo by sa aspoň jemne priblížiť pojem fraktálu. Pod fraktálom je chápaný útvar (podľa Benoit Mandelbrota - "otca" fraktálov ) s týmito vlastnosťami.

• je sebepodobný, t.j. ak daný útvar pozorujete v akejkoľvek mierke, stále vykazuje určitý charakteristický tvar.
• má neceločíselnú dimenziu, tj. dimenzia D je definovaná ako N = L^D, N je pocčet kópií pôvodného tvaru, pri L-násobnom zväčšení lineárneho rozmeru.
• má síce na pohľad zložitý tvar, no je generovaný jednoduchými pravidlami.

Jednou z možností generovania fraktálov je aj využitie formalizmu L-systémov. L-systém je tvorený nasledujúcou trojicou. Prvou je množina symbolov V, ďalej je to počiatočné neprázdne slovo A (axióma) a poslednou z trojice je množina pravidiel typu X --> S, kde X je symbolom a S je slovo. V tomto prípade ide o základnú definíciu tzv. bezkontextového L-systému (0L-systém). Ale vráťme sa k L-studiu a priblížme si základnú syntax pre zadávanie L-systému. Otvoríme nový projekt a v sekcii L-system zadáme nasledujúce

lsystem: 0
derivation length: 3
axiom: F--F--F
F --> F+F--F+F
endlsystem

Ak by sme v tomto momente spustili simulátor cpfg, výstup by bol negatívny a to z jednoduchého dôvodu. Pre zobrazenie obrazca je nutný kompletný reprezentačný rámec. Ale rozoberme si po poriadku jednotlivé riadky v sekcii L-studio.

lsystem: 0 - týmto výrazom formálne začíname nový L-systém a za dvojbodkou je nutné uviesť jeho meno.

derivation length: 3 - zadáva derivačný krok, tj. koľkokrát sa bude daný L-systém iterovať.

axiom: F--F--F - predstavuje počiatočné slovo L-systému, v tomto prípade ide o vygenerovanie trojuholníka, a to konkrétne. F - symbol reprezentuje pohyb o jednotku dĺžky, pričom za sebou zanechá úsečku a symbol - sa interpretuje ako otočenie na mieste doľava o špecifický uhol (v tomto prípade to bude uhol 60 stupňov).

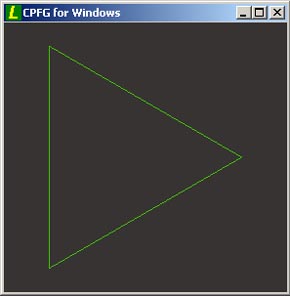
vizualizácia axiómy, tj. derivation step = 0

F --> F+F--F+F - ide o samotné pravidlo na prepisovanie symbolu F, ktoré vykoná následnú výmenu

endlsystem - formálne ukončuje zadaný L-systém

Pre správnu vizualizáciu a odsimulovanie je ďalej nutné doplniť nevyhnutné parametre tentoraz do sekcie View. Najdôležitejším je definovanie špecifického uhla. Na to nám v cpfg slúžia hneď dva parametre (použije sa iba jeden z nasledujúcich spôsobov).

• angle increment : hodnota, hodnota priamo udáva špecifický uhol, resp. jeho inkrementáciu.

• angle factor: hodnota, samotný uhol sa určí ako podiel 360/hodnota. (napr. pre uhol 60 stupňov, bude hodnota = 6).

ďalším z parametrov ktoré boli použité v tomto príklade je initial color: hodnota, kde hodnota určuje farbu z okna Colors ktorou sa bude daný L-systém vykresľovať.

Po definovaní L-systému môžeme pristúpiť k samotnej simulácii. Spustením cpfg dostaneme výsledok a vizualizáciu simulácie. Experimentovaním s parametrom derivation length, ktorý nadobúdal hodnoty 1,3,5, dostaneme nasledujúce výstupu z cpfg.

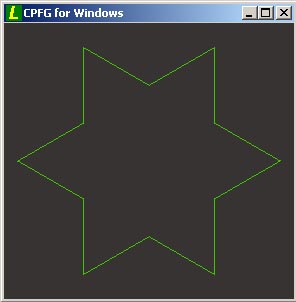
derivation length: 1

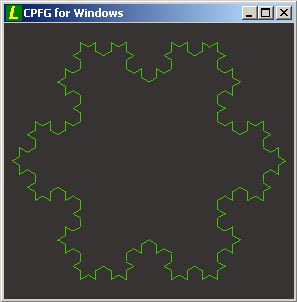
derivation length: 3

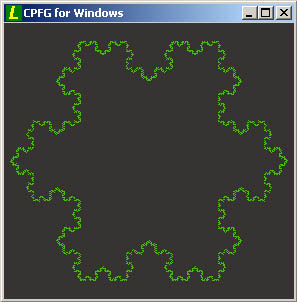
derivation length: 5

Ostáva ešte pripomenúť malý detail a to ak už je spustený Cpfg a nechceme ho stále reštartovať, potom všetky zmeny, urobené v L-studiu nadobudnú účinnosť použitím príkazov New model, New L-systém, New View z menu Cpfg.